|
���̖{��ǂ�ł��������F�l�� �@�@�@�傫�߂̕��i���A�������Ɣz�����ꂽ�^��ǃA���v�́A�܂�Łu�d�C�̂��炭��H�v�̂悤�ł��B �@�@�@�@�@�@�@����ȓd�C�̂����݂𗝉��������Ȃ�A�ȒP�����ȓd�C�̓��发���Ă݂܂����B �@�@�@�@�@�@�Ƃ��낪�ǂ̖{���A�ł������b�����̐������Ȃ��A��C�ɐ����ˑ��ւƈڍs���Ă��܂��܂��B�@�@ �@�@�@�@�@�@�@�܂����������̃C���X�g���A�C���X�g���[�^�[�ƒ��҂Ƃ̃����N���キ�A�[���ɋ@�\���Ă��܂���B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���̖{�ł́A���������̌����ӂ܂��A �@�@�@�@�@�@�@�@�@�@�@�@�Ƃ����_�ɐS�|�����A�d�C�̐��E�̒T���G�{��ڎw���܂����B |
![]()
�𗬂̎�ނ͂��낢�날��
�@
�d�r�ɒ�R���Ȃ��ƁA�������̕����ɓd��������A������Ƃ����܂��B
����d�r�̃v���X�ƃ}�C�i�X���Ђ�ς�ɂȂ������ēd���̌������s�����藈�����シ��Ƃ��A������𗬂Ƃ����܂��B
�܂��p��ł́A�������_�C���N�g�E�J�����g�iDirect Current�j�A������DC.
�𗬂̓I���^�l�C�e�B���O�E�J�����g�iAlternating Current)�A������AC.�@�Ƃ������܂��B
�𗬂͂��낢��ȃo���G�e�B��������āA���̔g�̌`�Ȃǂ��疼�O�����Ă��܂��B

�O�p�g�͎O�p�`�A���`�g�͎l�p�`�A�U�M�U�̃m�R�M���g�A�O�p�g�̏㉺�̂Ƃ���J�b�g����Α�`�g���ł��܂��B
�܂����`�g��g�ݍ��킹�ĊK�i�̌`�������K�i�g�����܂��B
���������Ƃ����Ă��𗬂̎���͐����g�ł��傤�B
���Ȃ݂Ɍ𗬂̗��_�͂�₱�����̂ŁA�G�W�\�����匙���������悤�ł����A�{���͂��̕����̉���ɒ��킵�܂��B
�@�@�@�y�S�z�����g�̖��O�͂������Ă���
�@�����g�́u�����v�Ƃ͂R�p���Ƃ������w�ɏo�錾�t�̂ЂƂŁA�T�C���i�������j�Ƃ������A�����g�̎����T�C���g�Ƃ������܂��B
�@�����������ɁA���̔g�`�̓s�A�m��M�^�[�́u���𐳂����v�e�������ȂǂɁA������O�̂悤�ɏo�Ă���A�ƂĂ��s�v�c�Ŏ��R�Ȑ����̔g�ł��B
�R�p���̐����Ƃ����̂́A���p�R�p�`�́@�Q�ӂ��g��������Z�̓����@�������܂��B�����ŁA��̓I�ȗ�������܂��傤�B
���p�R�p�`�̂R�ӂ̂����A�Q�̕ӂ͕����ʂ蒼�p�ɂȂ��Ă��܂��B
�����Œ��p�R�p�`�̐ςݖ��A�Εӂ����ɂ��Ȃ��悤�ɏ��ɒu���ƁA��ɂȂ�Εӂ̕����ƁA���Ɛ����ɂȂ�A�����ɂ�����ӂ������邱�ƂɂȂ�܂��B
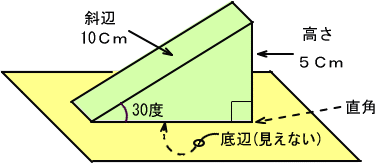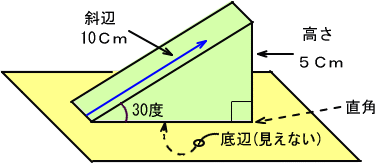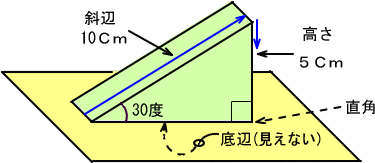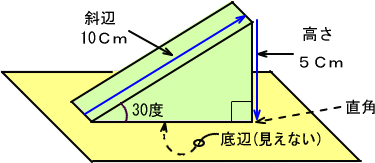
���̂Ƃ��A��̐}�̂悤�ȏ����ō������T�Z���`�A�Εӂ��P�O�Z���`�Ƒ��ꂽ�Ȃ�A
��������
�@�Ƃ������́A�@�Q�ӂ��g��������Z�̓����@�������Ƃ����킯�ł��B�����Łu�����́A�������Εӂ��B�v�Ƃ������Ƃ����ɂ����
��������������
���T�Z���`���P�O�Z���`
���O�C�T�@�@�@�ƂȂ�܂��B
�@���̎��́A�ΕӂP�O�Ȃ獂���T�A�܂�u�Εӂ̒������P�Ƃ��鎞�A�����͂O�C�T�ɑ�������B�v�Ƃ����ӓ��m�̔䗦��\���Ă��܂��B
�@����ɐ����͐��E���ʌ���Ȃ̂ŁA�����Ƃ����������������Ƃ����L���ŏ�����
���������O,�T�@�@�Ə����܂�
�@�ȏオ�@�@��قǂ̏����̃T�C���@�@��\���Ă���킯�ł����A���̂܂܂ł́@�@��قǂ̏����@�@�����i��ʁj���閼�O������܂���B
�@�����ŁA�ΕӂƏ��Ƃ̊p�x�x��ő���A���̌X���p�x���R�O�x�������Ȃ�A������T�C���̖��O�Ƃ��܂��B
�@����̏����ł́A�u�T�C���R�O�x�͂O��T���B�v�ƂȂ�A���Ƃ��ĕ\���@
�������R�O�����O,�T�@
����ŃT�C���ɖ��O�����܂����B���͒��p�R�p�`�ɂ͕s�v�c�Ȑ����������āA�Εӂ̌X���p�x������A
��������
�@�̓����i�䗦�j�����܂��Ă���Ƃ����̂ł����A�悭�l���Ă݂�ƁA����͂�����܂��Ȃ̂ł��B
�Ȃ��Ȃ�R�p�`�͂R������p�̘a���P�W�O�x�ł����A���p�R�p�`�͂��̂����P���X�O�x�Ȃ̂ŁA�c�����Q�̊p�x�̘a�͂X�O�x�ł��B
�����łǂ��炩�P���U�O�x�Ƃ킩��A�R�߂�
�X�O�x�|�U�O�x���R�O�x
�@�ƂȂ�܂��B�܂蒼�p�R�p�`�́A���p�ȊO�̂P�̊p�x�ŁA�R�߂̊p�x�����܂��Ă��܂����߁A�ӂ̑召�ɊW�Ȃ��A�S�ē����`�i�����`�j�ƂȂ�܂��B
�@���̌��ʕӓ��m�̔䗦�����܂��Ă��܂��̂ł��B
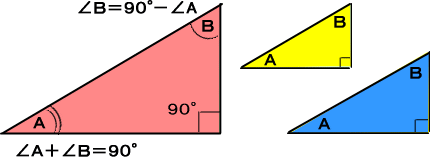
�Ⴆ�������S�T�x���l���鎞�A�����P�̊p�x��
�X�O�x�|�S�T�x���S�T�x
�@�܂�Q���ӎO�p�`�ɂȂ�܂��B
�@�Q���ӎO�p�`�̎Εӂ́A���̕ӂ́�Q�i���[�g�Q�Ɠǂ݁A��P�C�S�j�{�ł��邱�Ƃ��킩���Ă��܂��B
�@�����ō������T�Z���`�Ƃ���ΎΕӂ͂T�~��Q�Z���`�ɂȂ�܂�����A�������S�T����
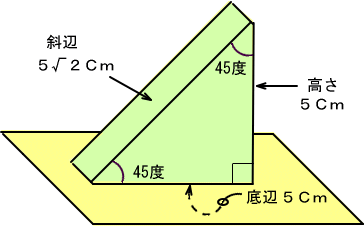
�@�������S�T�x����������
���T���T��Q
���P�^��Q
���P���P�C�S
���O,�V
�����ł���ɃC���[�W���Ă݂܂����A�Εӂƒ�ӂ̊p�x���O�x�̐ςݖ͂ǂ��Ȃ��Ă���̂ł��傤���B
���̂悤�ȂR�p�`�̐ςݖ́A���͂�ςݖƂ����܂���B
��������z�̐��E�ō���Ă݂�ƁA�Εӂƒ�ӂƂ���̂ɂȂ�A�����炭���ɒu�������̂悤�ɔ����A�����̕����͌���Ȃ��O�Z���`�ł��B
���̂��Ƃ���
�������������ΕӁ��O�Z���`���P�O�Z���`���O�@�ƂȂ�
�������O�����O�@�ł���Ƃ킩��܂��B
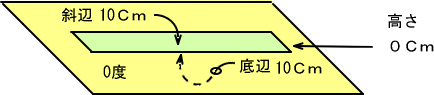
�܂��X�O�x�̂Ƃ��͎Εӂ����p�ł�����A�Εӂƍ����̕ӂ̕����Ƃ���̂ɂȂ�A�����P�������ɗ����Ă��銴���ɂȂ�܂��B
�܂�Εӂƍ����������Ȃ̂�
��������������
���P�O�Z���`���P�O�Z���`���P�@�ƂȂ���
�������X�O�����P�@�ł���Ƃ킩��܂��B
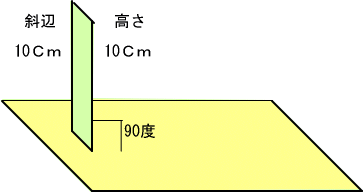
����ɂP�W�O�x����R�U�O�x�̊Ԃ͐ςݖ̍�̕��������̉��ɂ߂肱��ł����ԂŁA���͂�藧���������ł͂Ȃ����ݍ������ƂȂ�܂��B
�Ⴆ�Q�P�O�x�̏ꍇ�͂��̐}�̂悤�ɂȂ��Ă��܂��B
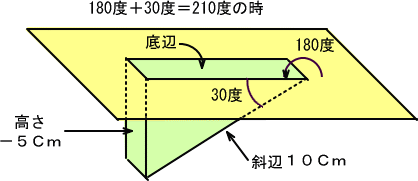
�����Ƃ��Ă̓}�C�i�X�̍����Ƃ������ԂɂȂ��Ă��܂�����A
�@�@�@�@�@�@��������������
�@�@�@�@�@�@���|�T�Z���`���P�O�Z���`
�@�@�@�@�@�@�@���|�O��T
�����Ł@�@�@�@�@�@�������Q�P�O�����|�O��T�@�ƂȂ�܂�
����ɂ���ɂQ�V�O���̎��̍����̓}�C�i�X�P�O�Z���`�Ȃ̂�
�\�P�O�Z���`���P�O�Z���`���|�P�@�@�ƂȂ���
�������Q�V�O�����|�P�@�@�ł���Ƃ킩��܂��B
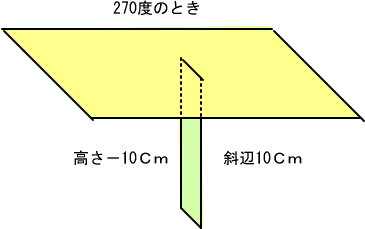
�����g���G�ɕ`�����Ƃ���ƁA���̎p�͍�����E�ɂЂ����P�{�̒����ɉ����āA�㉺�ɔg�ł��̌`�����Ă��܂��B
�g�̍����͒����オ�O�A�����̏㕔���v���X���A���̓}�C�i�X���Ƃ��܂��B
�܂��A�����̍��[���O�x�ƌ��߂āA��������E�Ɍ������āA�ϓ��ɂP�x���x���̖ڐ������Ă����܂��B
������1�x�Â������ނƁA�������ݓ����ĕ�����Â炭�Ȃ邽�߁A�R�O�x�Ԋu�ŏ����Ă���܂��B
�@�@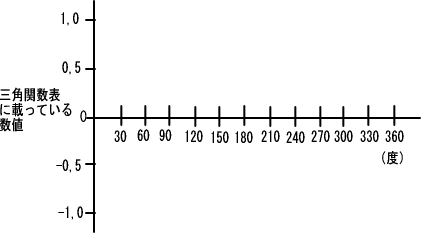
�ł͂��̒����ɉ����āA�����g��`���čs���܂��傤�B�܂��X�^�[�g�n�_�͂O�x�ł��B
�T�C���O�x�͂O�Ȃ̂Ŕg�̍����͂O�܂蒼���Ɠ����Ƃ���ł��B
���ɒ��Ԓn�_���ȗ����ĂR�O�x�̖ڐ��܂ł���ƁA�T�C���R�O�x�͂O,�T�Ȃ̂łO,�T�̍����ɂȂ�܂��B
���̂Ƃ��u�O,�T�v�̂��Ƃɂ���P�ʂ͉��ł��ǂ��A�傫���G��`������������A�O,�T���[�g���A�������G�Ȃ�O,�T�Z���`�ł��܂��܂���B
�@�@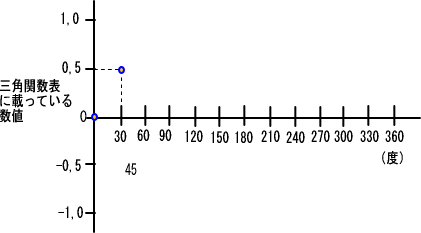
�܂��u�P�v���@�P�O�Z���`�@�Ƃ��ĕ\���@�u�O,�T�v�@�͂T�Z���`�ɑ������āA�`���̂Ɏ育��ȃT�C�Y�ƂȂ�܂��B
�R�O�x�́@�O,�T�@�ɑ����ā@�S�T�x�ł́@�T�C���S�T�x���P�^��Q���O,�V�@�Ƒ����A�U�O�x�Ł@��R�^�Q���O,�W�V�@�A�X�O�x�ōő�̂P�ɂȂ�܂��B
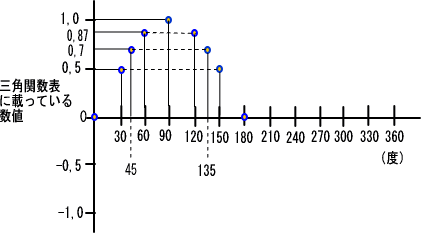
�X�O�x����ƍ��x�͉�����n�߂܂����A��͎����悤�ȌJ��Ԃ��Ȃ̂ŁA
�@�O�p���\�@�́@�u��蔲���Łv�@�������Ă݂܂���
| �p�@�x | �T�C�� | �p�@�x | �T�C�� |
| �O�� | �@�@�O | �P�W�O�� | �@�@�@�O |
| �R�O�� | �@�@�O,�T | �Q�P�O�� | �@�@�|�O,�T |
| �S�T�� | �@�@�O,�V�P | �Q�Q�T�� | �@�@�|�O,�V�P |
| �U�O�� | �@�@�O,�W�U�U | �Q�S�O�� | �@�@�|�O,�W�U�U |
| �X�O�� | �@�@�P,�O�O�O | �Q�V�O�� | �@�@�|�P,�O�O�O |
| �P�Q�O�� | �@�@�O,�W�U�U | �R�O�O�� | �@�@�|�O,�W�U�U |
| �P�R�T�� | �@�@�O,�V�P | �R�P�T�� | �@�@�|�O,�V�P |
| �P�T�O�� | �@�@�O,�T | �R�R�O�� | �@�@�|�O,�T |
| �P�W�O�� | �@�@�O | �R�U�O�� | �@�@�@�O |
���̂悤�ɂR�U�O�x�܂ł��P�����A�܂��͂P�T�C�N���ƌ����A��͂��̌J��Ԃ��ɂȂ邽�߁A�Q�{�̂V�Q�O�x�ł��R�{�̂P�O�W�O�x�ł������ł��B
�������A���������|�C���g���Ȃ��������ł́A�J�N�J�N�����g�`�ɂȂ��Ă��܂��܂��B
�����łP�x�Â̐��l���L���Ă���O�p���\���g���A�O�x����R�U�O�x�܂ōׂ������l�����āA�Ȃ߂炩�Ȑ����g�̔g�`��`���o���܂��B
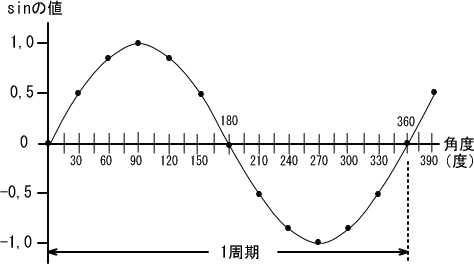
�b�j�����g�𐔎��ƋL���ŏ���
�g�̍����́A�C�ʂ����Ă��킩��悤�ɁA���Ƌ��ɍ����Ȃ�����Ⴍ�Ȃ����肵�Ă��܂��B
�����獂���O���̎��̔g�����āu���̔g�̍����͂O���ł��B�v�Ȃǂƌ����Ă��A���̏u�Ԃɂ͂��͂�ʂ̍����ɂȂ��Ă��܂��B
�����Ŏ��Ƌ��ɕω�����g�̍����𐳊m���\�����߁A��قǂ̒�����̓x�������p���܂��B
������ɂ����ڐ��̂P�����A���Ȃ킿�O�x����R�U�O�x�܂ł̊Ԃ��A���i�V�[�^�j�Ƃ������O�̓_���ړ����čs���ƁA
���̂���ꏊ�Ő����g�̍����͂��������ƂȂ��Ă��܂��B
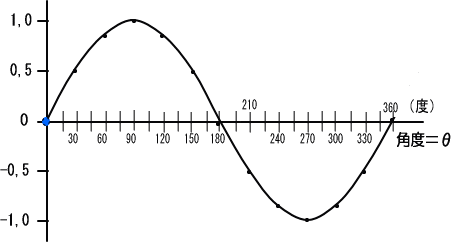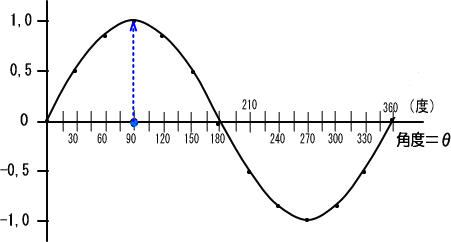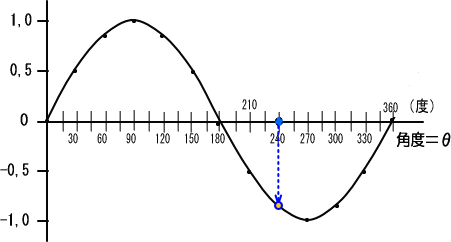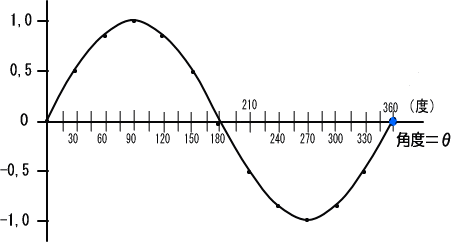
�Ⴆ�A�����O�x�Ȃ�@
�@�@�@�@�@�@�@�@�����������������O�����O
�܂������O�x�Ȃ琳���g�̍����͂O�ƂȂ�܂��B
�܂������X�O�x�Ȃ�@
�@�@�@�@�@�@�@�@�@�����������������X�O�����P
�@�܂������X�O�x�Ȃ琳���g�̍����͂P�ƂȂ�܂��B
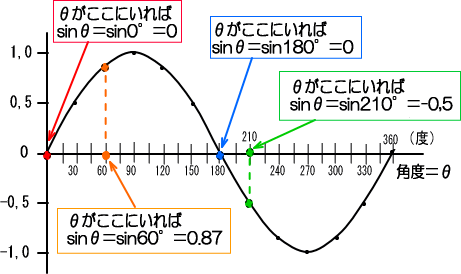
���̂悤�ɍl����ƁA���������Ƃ�����������A���������̂ǂ��ɂ��悤�ƁA���̎��́A�g�̍������킩���Ă��܂����ɂȂ�܂��B
�@�܂�u���������̍����������g�v�Ƃ������R����A���̔g�𐳌��g�i�T�C���g�j�ƌĂ�ł���̂ł��B
�Ƃ���Ő�قǁA���Ƌ��ɕω�����g�ƌ������ɂ�������炸�A�x���̘b�肵���o�Ă��Ă��܂���B
�m���ɓx���́A���̂܂܂ł͎��Ԃ������܂���B
�����������g���P�����A�܂�O�x����R�U�O�x�܂ŕω����鎞�Ԃ��P����P�b�Ƃ���A�u�P�x�v�Ƃ͂��̂P�^�R�U�O�ɑ�������u���ԁv�ɂȂ�܂��B
�ł͗�������Ă��낢��ȏu�Ԃ̔g�̍�����\�����Ă݂܂��傤�B
�@�@�@�@�@�@�@�@��P�j
�����g���X�^�[�g�O�x����R�O�x�i�Ƃ��A�g�̍����͐�قǂ̕\����
�@�@�������R�O�����O,�T
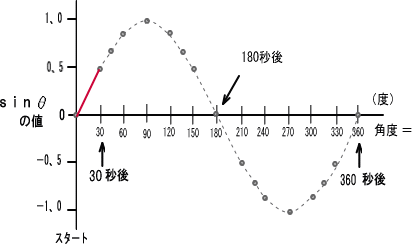
�@�@�@��Q�j �P�����R�U�O�b�����鐳���g�ł́A�R�U�O�b�łR�U�O�x�i�ނ̂ł�����P�x�͂P�b�ɂȂ�A�X�^�[�g����R�O�b���ƂR�O�x�i��ł��邱�ƂɂȂ�܂��B
�@�@�@�@�@�@�@�@�@�@�@�@���̎��A�g�̍�����
�@�@�@�@�@�@�������R�O�����O,�T
�@��������ۂ̔g�`�Ō��Ă݂�Ǝ��̐}�̂悤�ɂȂ�܂��B
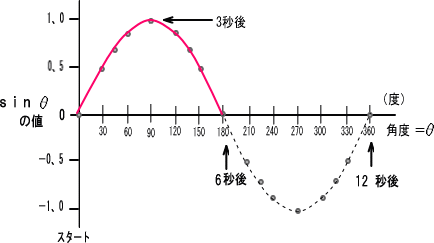
�@�@�@�@�@�@�@��R�j �P�����P�Q�b�̐����g���X�^�[�g����U�b���ƂP�����̔����̂P�W�O�x������A�g�̍�����
�@�@�@�@�@�@�������P�W�O�����O
�@�@�@���ۂ̔g�`�ł�������Ă݂܂��傤�B
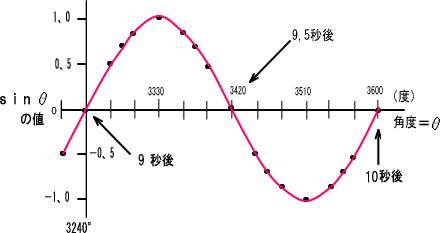
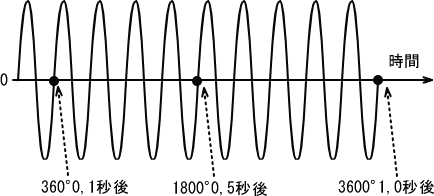
�@�@�@��S�j �P�����P�b�̐����g���P�O�b���ƂR�U�O�O�x�܂肿�傤��
�@�@�@�@�@�@�@�@�@�@�@�P�O�����ڂ��I���ăX�^�[�g�ʒu�ɖ߂��Ă��邩��A�g�̍����͂O
�@�@�@�@�@�@�������R�U�O�O�����������R�U�O�����O
�@�@�@�@�}�ł̓X�^�[�g�n�_����X�b��܂ł͏ȗ����ĕ`���܂����B
���̂悤�ɂ��āA�@�@�@�@�@�@�@�@
�@
| �@�@�@�@�@�@�P�����ɂ����鎞���ƁA �@�@�@�@�A�@�ǂ̂��炢���Ԃ��o�������������ɁA �@�@�@�@�B�@���������Ƃ����������i���p�x�j�����x�ɂȂ��Ă��邩�A |
�@����ׂ�A�g�̍������\������鎖���������Ă��܂����B
�������A����Ȃɂς��Ɠ������o��̂́A��̗�̂悤�ȕ�����₷���ꍇ�ɂ�����A���ʂ͎O�p���\�̂����b�ɂȂ�܂��B
�@�@�y�T�z�@�����g�͂��낢��ȉ��̌�
�����g�̉������ŕ����ƁA�����̍����ɂ��A�s�[�Ƃ��|�[�Ƃ����[�ȂǂƃJ�h�̂Ȃ����ł��B
���������ꂪ����ނ�������ƁA����M�[�Ƃ��r�[�Ƃ��u�[�ȂǗl�X�ȉ��F�ɕω����܂��B
�����Ď������������땷���Ă���l�X�ȉ��́A���낢��ȉ����̐����g�����G�Ƀ~�b�N�X���ꂽ���̂Ȃ̂ł��B
�`�j�����g�̎��g���Ƃ�
���낢��ȉ����̐����g�����܂�����킷���@�͂Ȃ��ł��傤���B
�����Łu�s�[�v�ƕ������������A�P�b�ԂɂP�O�O�O�����܂�P�O�O�O���C��U�������Ă��鉹�Ȃ�A������P�O�O�O�w���c�܂��͂P�L���w���c�̉��ƕ\�����܂��B
�@�@�@�@�w���c�̓h�C�c�̕����w�҂ŁA�d�g�����܂����B
�ӂ������g�͂P�b�Ԃɉ��������J��Ԃ����Ƃ����A���g���Ŕ��ʂ��܂��B
�܂��w���c�́u�g���v�ƌ����L���ŕ\���A�L���w���c�́u�j�g���v�ŕ\���܂��B
�a�j�����g�����g���̂킩�鐔���ƋL���ŏ���
�ŏ��͂P�b�ԂɂP��U������P�g���̗�ōl���܂��B
���̂Ƃ��P�����܂�O�x����R�U�O�x�܂ŁA���i�V�[�^�j�Ƃ������O�̓_���ړ����A���傤�ǂP�b�Ԃōs�Ȃ��܂��B
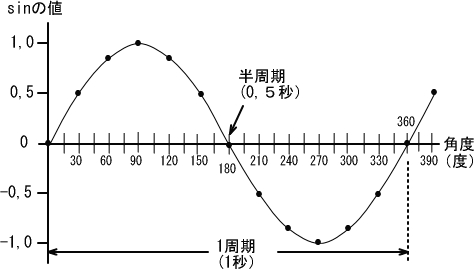
�ł͂P�b�̂��傤�ǔ����A�O��T�b��̔g�̍����͂ǂꂾ�����ƌ�����
�@�@�@�@�@�@�@�@�@�@�������i�R�U�O���~�O,�T�j���������P�W�O�����O
�@���̂Ƃ��A�g�͂��傤�ǂP�W�O���܂Ői�݁A�O�̍����̂Ƃ����ʉߒ��ł����B
�@�@
�Ƃ���Ŋp�x�ɂ́@���i�p�C�j�@�Ƃ����L���ɂ��\����������A����ɂ������Ƃ͂P�W�O�x���Ӗ����A�R�U�O�x�́@�Q���@�ɂȂ�܂��B
������g���Đ�قǂ̎���������
�@�@�@�@�@�@�@�@�@�@�@�@�@�������i�R�U�O���~�O,�T�j
�@�@�@�@�@�@�@�@�@�@�@���������i�Q���~�O,�T�j
�@�@�@�@�@�@�@�@�@�@�@����������
�@�@�@�@�@�@�@�@�@�@�@���O�@�@�ƂȂ�܂�
�@�Â��ĂP�b�ԂɂP�O��U������P�O�g���̂Ƃ��̂O,�T�b����l���Ă݂܂��B
�@�P�b�ԂłP�O�����Ƃ������Ƃ́A�R�U�O���~�P�O���R�U�O�O���̖ڐ��܂Ŕg���`����Ă��܂��B
�@�����łO,�T�b��̔g�̍�����
�@�@�@�@�@�@�@�@�������o�i�R�U�O���~�P�O�j�~�O,�T�p
�@�@�@�@�@�@�@�@���������i�R�U�O�O���~�O,�T�j
�@�@�@�@�@�@�@�@���������P�W�O�O��
�@�@�@�@�@�@�@���������i�R�U�O���~�T�j
�@�@�@�@�@�@�@�@�@�@�@�@�@���O
�@�p�x�̐��l�͑傫���Ă��A���ǂ͂T��ڂɂ����R�U�O���Ƃ��������ŁA�g�̍����͌��ɖ߂��ĂO�ł��B
�@����������g�������
�������i�Q���~�P�O�~�O,�T�j�@�@�@�ƂȂ�܂��B
�@����Ɏ��g�����������āA�P�L���w���c�͂P�b�ԂɂP�O�O�O�����ł��B
�@�܂����b��̒l�ׂ邩�͌�Ō��߂邱�Ƃɂ��āA���ɂ��b��Ƃ�����
�@�@�@�@�@�������i�R�U�O���~�P�O�O�O�~���j�@�@�ƂȂ�܂��B
������ �� �Ƃ����L����p�����̂́A�����ɓ��鐔�������b��Ƃ������ԁi�^�C���j������ł��B���̎��������g����
�@�@�@�@�@�������i�Q���~�P�O�O�O�~���j
�������ĂR�̗���݂�ƁA�Q���̌�ɂ͂P�b�Ԃ̎����̉A�܂���g����������Ă��鎖���킩��܂��B
�����ŁA���g�������Ƃł��낢��ς�邱�Ƃ��l���A���̕������A���g�����Ӗ�����t���P���V�[�̋L�����ɒu���������
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�������i�R�U�O���~���g���~���b��j���������@�Q���@���@���@�b�@�@�@�@�@�ƂȂ�܂��B
|
�@�@�@�w�܂����g�����ƒ��ׂ������Ԃ��ɐ��l�Ă͂߂Ċ|���Z���A �@�@�@����ɂQ���Ƃ����p�x���|���A�o�Ă������l�i���p�x�j���v�Z���܂��B �@�@�@���ɂ��̊p�x���O�p���\�Œ��ׂ�A���g�����̐����g���X�^�[�g���Ă��b��A �@�@�@�ǂ�Ȕg�̍����ɂȂ��Ă��邩���A�\�������ł��܂���B�x�ƌ������ɂȂ�܂��B |
�@�܂��g�̍�����g���l�Ƃ����܂��B�����ł��낢��Ȏ��g���̐����g�̏u�Ԃɂ�����g���l���v�Z���Ă݂܂��傤�B
�@�������g���l�́A�ő�ł��r�����X�O���̂P�܂łł����A�ŏ��ł��r�����Q�V�O���̃}�C�i�X�P�܂łł��B
�@�@�@�@�@�@��P�j�P���g���̐����g���X�^�[�g���ĂO,�T�b���������̔g���l���v�Z�����
�@�@�@�@�������i�Q���~���~�� �b�j���������i�Q���~�P�O�O�O�~�O,�T�j
�@�@�@�@�@�@���������i�Q���~�T�O�O�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���������O��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���O
���̏u�Ԑ����g�͂��傤�ǂT�O�O�����ڂ̂R�U�O�x�̂Ƃ����ʉߒ��ł��B
���ɑ�Ȃ̂́A���̂Q�Ԗڂɂ���Q���~�T�O�O�Ƃ���������菜�������ł��B
�Ȃ����̂悤�Ȃ��Ƃ��o���邩�ƌ����A�Q���̐����{�́A�P�����̌J��Ԃ��ɉ߂��Ȃ��̂ŁA�O���Ɠ������Ƃ��Ӗ����Ă��܂��B
�����ŁA�����ȒP�ɂ��邽�߂��̕����͖������܂��B
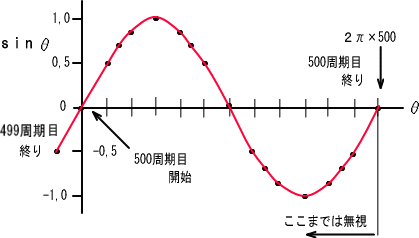
��Q�j�P�j�g���̐����g���X�^�[�g���ĂP�^�P�U�b���������̔g���l��
�@�@�@�@�@�@�@�@�@�@�@�@�@�������i�Q���~���~�� �b�j
�@�@�@�@�@�@�@�@�@�@�@�@�@���������i�Q���~�P�O�O�O�~�P�^�P�U�j
�����łQ���J�b�R����o���܂��B
����Ɏc���������ł���P�Ȃ�J��Ԃ��̐��������ƁA�����ł��Ȃ����������ɕ����邽�߁A�ѕ����ɂ����
�@�@�@�@�@�@�@�@�@�@�@�@�@���������Q���i�Q�T�O�^�S�j
�@�@�@�@�@�@�@�@�@�@�@�@�@���������Q���i�U�Q�{�Q�^�S�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@��������{�i�Q���~�U�Q�j�{�i�S�^�S�j}
���̎��̈Ӗ��͂Q�����U�Q�������P����Ƃ������ł�����A�U�Q�����̌コ��ɂP�W�O�x�i��ł����ԂɂȂ�܂��B
�����łU�Q�����͖������āA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@����������
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���������P�W�O��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���O�@�@�ƂȂ�܂��B
�@�����}�ŕ\���Ǝ��̂悤�ɂȂ�܂��B
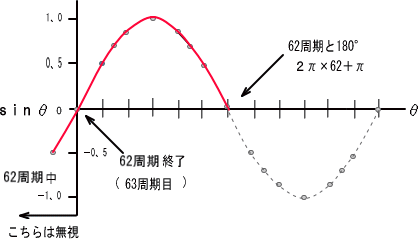
�@�@�@�@�@��R�j �Q�j�g���̐����g���X�^�[�g���ĂP�^�R�b���������̔g���l���v�Z�����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�������i�Q���~�Q�O�O�O�~�P�^�R�j
�@�@�@�@�@�@�@�@�@�@�@�@�@���������Q���i�Q�O�O�O�^�R�j
�@�@�@�@�@�@�@�@�@�@�@�@���������Q���i�U�U�U�{�Q�^�R�j
�@�@�@�@�@�@�@�@�@�@�@�@�@��������{�Q���~�U�U�U�{�i�S�^�R�j}
�@�����ł��U�U�U�����͖�������
�@�@�@�@�@�@�@�@�@�@�@�@�@���������i�S���^�R�j
�@�@�@�@�@�@�@�@�@�@�@�@�@���������Q�S�O��
�@�@�@�@�@�@�@�@�@�@�@�@�@���|��R�^�Q
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���|�O,�W�V
�P�̊p���Q�S�O�x�̒��p�O�p�`�͂Q�S�O���P�W�O�{�U�O���Ȃ킿�������������Œ�ӂƂ͂U�O�x�̎Εӂ������܂��B
���̒��p�R�p�`�͂R�ӂ̒����̔䗦���A��ӂ��P�Ƃ���ƎΕӂ͂Q�ŁA�����́�R�Ƃ킩���Ă��܂��B
���̏�Ԃ̐ςݖ͂��̂悤�ɂȂ�܂��B
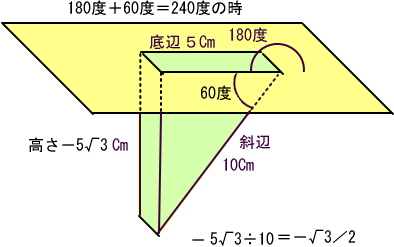
�������������Ȃ̂ŁA�����́|��R�ɂȂ�܂��B�܂��Εӂ͒P�Ȃ钷���Ȃ̂Ō����͊W�����A�����L���̓v���X�ł��B
�����ŎO�p���\���g��Ȃ��Ă��������Q�S�O���͂������U�O���̋L�����}�C�i�X�ɂȂ����[��R�^�Q���\�O�C�W�U�U�Ƃ킩��܂��B
�g�`�̗l�q��}�ɂ��Ă݂܂����B
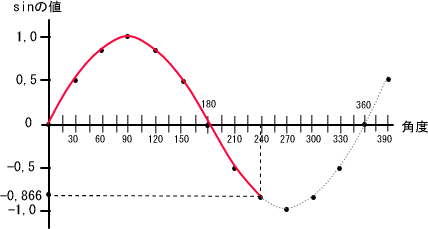
���̂悤�ɂ��āA���Ƌ��ɕω����邳�܂��܂Ȏ��g���̐����g�̔g���l��
�@�@�������Q�����E���b�@�@
�@�Ƃ��������ƋL���ŏ����鎖�ɂȂ�܂����B
C)�@�����ɂ���
�@�@�������ǂ��l���Ă݂�Ƃ������̌�ɏ�����鐔���́A�{���p�x�Ƃ��̔{�������̂͂��ł��B
�����Ɏ��Ԃ̒P�ʁu�� �b�v������̂͂��������̂ł͂Ȃ��ł��傤���B
�����Ő��w�̌��܂�̈�u�����v�ɂ��Ēm���Ă����Ȃ���Ȃ�܂���B
�Q�Ƃ��R�͐��̑傫����\���Ă��܂����A���̂��ƂɒP�ʂ��t���ƈ��̗ʂ�\���܂��B
�P�ʂ��t���������͂��́u�����v�������ƂɂȂ�A�v�Z�̒��ŏ���ɏ������Ƃ��o���܂���B
�Ⴆ�P���i���[�g���j�́u���v�Ƃ��������̎��������̂ŁA�v�Z���鎞��
�@�@�@�@�@�S�����Q���Q���@�@
�Ɠ����Ɏ������c��܂��B���̎��͂S�����Q�ɕ�������ƂQ���ɂȂ�Ƃ����Ӗ��ł���
�@�@�@�@�@�@�@�@�@�@�@�@�@�S�����Q�����Q�@�@
�Ƃ����v�Z�́A�������玟���������Ă��܂��B���̎��͂S���̒��ɂQ�����Q����Ƃ����Ӗ��ł��B
���̂Ƃ������̎����ł��邍���m��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@���������P�@�@�Ƃ������Ŋ���Z���ł��Ă��邱�ƂɂȂ�܂��B
�܂����Ԃ������̂ЂƂ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�S�b���Q���Q�b�@�@
�Ƃ������́A�S�b�̔����̎��Ԃ͂Q�b�Ƃ����Ӗ��ł���
�@�@�@�@�@�@�@�@�@�@�@�@�@�S�b���Q�b���Q�@�@
�Ƃ������́A�S�b�̒��ɂ͂Q�b�Ƃ������Ԃ��Q��Ƃ������ƂŁA���Ԃ̎����ł���b���m�������ē�����������Ă��܂��B
�����ł��i���g���j�̈Ӗ����l���Ă݂܂��ƁA���g���Ƃ͂P�b�Ԃɉ��������邩���Ӗ����Ă��܂��B
�@�Ⴆ�Ή��̐}�́@�P�b�ԂɂP�O�����@�̏ꍇ�ł��B
| �P�b�ԂɂP�O�����̏ꍇ �@�@�@  |
�܂��A�P�O�b�ԂɂQ�O�����ω����鐳���g���P�b�Ԃɕω���������̉�
�@�@�@�@�@�@�@�@�����Q�O�P�O�b
�@�@�@�@�@�@�@�@���Q�P�b
���̂悤�ɂ��ɂ́i���P�b�j�Ƃ����������t���܂��̂ŁA���g���Ƃ͒P�Ȃ�ł͂Ȃ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�������P�b
�@�@�@�@�@�@�@�@�@�@�@�@�@�@���^�P�b�@�@
�Ƃ����A����Ɏ��Ԃ̎����̕t�������l�Ȃ̂ł��B
�����Ŏ��g���@�u�@���@�v�@�̎����܂�́A�T�C�N���́@�u�@���@�v�@�ŕ\���u�b�v�͉p��̂r�d�b�n�m�c�́@�u�@���@�v�@�ŕ\����
�@�@�@�@�@�@�@�@�@�@�����^�P�b����/���@�i�T�C�N���@�p�[�@�Z�J���h�j
�@�@�@�@�������Q���@�@���@�@���@���@���@�������Q���@�~�@���@/�@���@�~�@���@�@���@���������Q������
�@�Ƃ������ƂŁA�Q���� �� �b�@�́A�R�U�O�x�ł���@�Q���@�� �� �� �{�@���������̏����Ȋp�x�ƂȂ�܂����B
�@����ɂ����������ΐ����g�̎��Ƃ�
�@�@�@�@�@�@�@�@�@�@�@�@�u�������i�R�U�O�x�~�{���j�v�@�@�@�@�@�Ƃ������ɒP���Ȏ��ł����Ȃ��̂ł��B
�@�@�@�y�U�z�𗬂��I�[���̖@���Ɠd��
�����g�͉������łȂ��d���ɂ����Ă͂܂�܂��B�𗬓d���������d���Ɠ����d�C�Ȃ̂ŁA�I�[���̖@���ɏo�Ă����|���Z
�d���@�h�@�~�@��R�@�q�@���@�d���@�d
�͂������A���̂Q�̊���Z�����Ȃ肽���܂��B����ɓd�͂��������l��
�@�@�@�@�@�@�@�@�d���d�@�~�@�d���@�h�@���@�d�́@�o�@�ŒP�ʂ͂v�i���b�g�j
�ƂȂ�܂��B�d�C�̂��Ƃ́A�����ł͓d�r������܂����A�𗬂̓d�r�Ƃ����͖̂����̂Ō𗬓d�����g���܂��B
�@�@�@�y�V�z�𗬂̓d��
�𗬓d���ň�Ԑg�߂Ȃ͉̂ƒ�̃R���Z���g�ł��傤�B�R���Z���g����Ƃ��𗬂͂P�O�O�{���g�ŁA�֓��Ȃ�T�O�g���ł��B
�����ō��܂ŏK�������Ƃ��g���āA�R���Z���g�̌𗬓d��������킵�Ă݂��
�������Q���� �� �����������i�Q�~���~�T�O�~���j�E�E�E���̉E�ӂ͂��̒��ɂ��� �P�^�� �� �� �� �� �� ���ł����������Ă��邱�Ƃɒ���
�@�Ƃ��낪����ɂ͂ǂ��ɂ��P�O�O�{���g�̎��������Ă��܂���B
�@�܂荡�܂Ŏ����Ă����g���l�u�O��T�v�Ƃ��u�O��V�v�͂P�{���g����ɍl���Ă����̂ł��B
�@�ł�����P�O�O�{���g�̂Ƃ��͑S�̂��P�O�O�{����
�@�@�@�@�@�@�@�@�P�O�O�~�������i�Q���~�T�O�~���j
�@�ƂȂ�܂��B�����łP�O�O�u�Ɍ��炸�A���낢��ȓd����\�����Ƃ��l���Ă������̑O�ɂ���d���̐������u�`�v�ƒu��������ƁA���̎���
�@�@�`�E�������Q���� �� ���@�ƂȂ�܂��B
�@����ōō��u�`�v�{���g�Ŏ��g���u���v�̐����g�́u���v�b��̔g���l�́A�ǂ��Ȃ��Ă��邩�Ƃ����A�����g�̂قƂ�ǑS�Ă̏�킩��悤�ɂȂ�܂����B
�@�Ⴆ�Ύ��g�����ł`�̒l���P�u�ƂQ�u�̐����g�ł���
�@�@�@�������Q���� �� ���@�Ɓ@�Q�E�������Q���� �� ��
�@�̐}��`���Ǝ��̂悤�ɂȂ�܂�
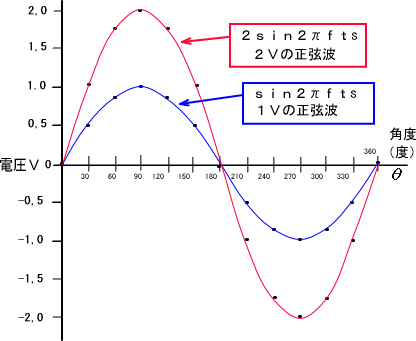
�����Ŏ��g���P�j�g���A�d���P�O�u�̐����g���ɂƂ��āA�����ŕ\���Ă݂�ƁA
�@�@�@�@�@�@�@�@�@�@�@�`�E�������Q������ �����P�O�E�������i�Q���~�P�O�O�O ���j
�@���̎��̉E�ӂ������Ӗ��́A�u�ő�d�����P�O�u�ŁA�P�����R�U�O�����P�b�ԂɂP�O�O�O��J��Ԃ��Ă��鐳���g�́A�� �b��̔g���l�������B�v
�@�ƌ������ɂȂ�܂��B
�@�@�@�y�W�z�s�[�N�l�Ǝ����l
�`�j�s�[�N�l
�P�O�O�u�̒����ƂP�O�O�u�̌𗬁i�����g�j���ׂ�ƁA�������Ɍ𗬂͂X�O���łP�O�O�u�ł���A�Q�V�O���Ń}�C�i�X�P�O�O�u�ł����A
�O����P�W�O����R�U�O���̎��͂O�u�ɂȂ��Ă��܂��B
�@�܂��O�u�̕t�߂��P�O�O�u�ɂ́A�͂邩�Ɏ����Ă��܂���B
����Œ����Ɠ����P�O�O�u���ƌ�������A�������������͓������A���Ƃ͓K���ɂ��x�݂��Ă���l�ƁA
�S���x�݂Ȃ������Ă���l�ɁA����������n���Ă���悤�Ȃ��̂ł��B
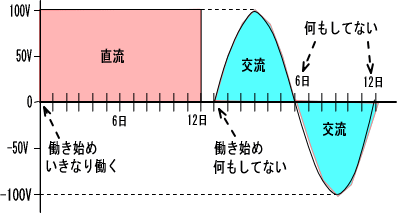
�����ŌĂѕ���ς��A�𗬂̏ꍇ�́u�s�[�N�l���P�O�O�u�ɂȂ��Ă���B�v�ƌ����܂��B
�����l�Ƃͤ�{���͂ǂꂾ���d���������̂�������悤�ɂ��邱�Ƃ�ړI�Ƃ��܂�����A�d�͂𒆐S�ɍl���܂��B
�����Œ����̂Ƃ��Ɠ����悤�ɂP���̒�R���@��̂����ɂȂ��A�𗬂̓d���̓s�[�N�l�P�u�̐����g
�d���d=�r�����Q���� �� ���i�u�j

�@���g���܂����u�Q���������v�͒P�Ȃ�p�x�ɉ߂��Ȃ����Ƃ���A�����ȒP�ɂ��邽�߁A�P���Ȋp�x�̋L���u���v�Ƃ���������
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�Q���� �� �������@�@
�@�Ƃ��邱�Ƃ��d���́@�@�@�@�@�@�@�������Q���� �� ���i�u�j���炓�������i�u�j�@�Ə����������܂��B
�@�܂��d���h���I�[���̖@�����g���A�d���i���������i�u�j�j����R�i1���j�@����v�Z����ƁA
�@�@�d�������������i�u�j���P�i���j�����������i�`�j
�@�������ēd���h�Ɠd���d�����܂����Ƃ���ŁA�d�͂o�͂d�~�h�ł�����
�@�@�@�@�@�@�@�@�d�͂o�����������i�u�j�~���������i�`�j
�@�ł��B�����ŒP�ʂ��ȗ����Ă݂�ƁA���������~���������Ƃ������������ǂ����̊|���Z���ł܂����B
�@�������A���̒��ɂ͓��̂����l�������Ƃ��āA���w�҂ɂ��
| �������Q����1-�Q������2�Ɓ@�E�E�E�@�{�p�̌��� �Ƃ����̂������āA�����ό`���� �@�@���������~�����������i�P�|�������Q���j�^�Q�@�@�@ |
�@�@�@�@�@�@�@
�@�Ƃ������������łɗp�ӂ���Ă��܂��B���̎����̖ōX�ɕό`�����
�@�@�@�@�@�@�@�@�@�@�@���i�P�^�Q�j�|�i�P�^�Q�j�E�i�������Q���j�@
�@�ƂȂ�܂��B����Ɂu���v��{���́@�u�Q���� �� ���v�@�ɏ����Ȃ����Ɓ@�u�Q���v�@�́@�u�Q�~�i�Q���� �� ���j�v�@�Ə����܂��B
�@�Ƃ��낪��������̂܂܌v�Z���ā@�u�S���� �� ���v�@�Ə����Ă��A���̎����ǂ�������܂���B
�@�����Łu�Q���E�Q�� �� ���v�Ə����A�� ���Q�{�ɂȂ����A�܂���g�����Q�{�ɂȂ������Ƃ�������ł��傤�B
�@���̏������ɉ����Ă��Ď���W�J����ƁA
�@�@�@�@�@�@�@���������~�����������i�P�|�������Q���j�^�Q
�@�@�@�@�@�@�@�@�@�@���i�P�^�Q�j�|�i�P�^�Q�j�E�i�������Q���j
�@�@�@�@�@�@�@�@�@�@���i�P�^�Q�j�|�i�P�^�Q�j�E�i�������Q���E�Q �� �� ���j�@�@�@
�@���̏�ԂŎ����R�ɐF�������āA�������ƂɌ��Ă݂܂��B
�@���̎��������ŏ����@ �@�i�P�^�Q�j �@�@�@�Ƃ́u�O���t�̐��S�̂��O��T�����v���X���Ɏ����グ�܂���B�v�Ƃ������Ƃł��B
�@�Ƃ肠�������v�Z�̏��ԏ�A�@ �@�i�P�^�Q�j�@ �@�����ɒu���Ƃ����
�@�@�@�@�@�@�@�@���@�|�@�i�P�^�Q�j�@�@�@�~�@�i�������Q���Q �� �� ���j�@�@�@�{�@�i�P�^�Q�j�@
�@�Ə����܂��B�����Ŏ���
�@�@�@�@�@�@�@�@�@�@�@�|�i�P�^�Q�j�@�@�~�@�i�������Q���Q �� �� ���j�@�@�@���Ɋm���߂܂��B
�@�܂��@�@�@�@�@�@�@�@�|�i�P�^�Q�j �@�@�Ƃ����̂̓}�C�i�X�Q���̂P���|����Ƃ����P���ȈӖ��ł��B
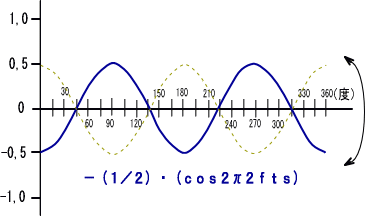
�@���́@�@�@�i�������Q���Q �� �� ���j�@�@�@�@�Ƃ��������G�ɕ`���Ă݂�ƁA�g�̌`�͐����g�Ƃ܂����������`�ł��B
�@�قȂ�̂́A�O���̂Ƃ��ɂP�A�܂萳���g�̂X�O���̂Ƃ�����n�܂�悤�Ȍ`�������T�C���g�ɗǂ�����
�@�@�@�@�@�@�@�@�@�@�@�@�@�]���g�i�R�T�C���g�j�@�@�@�@�@�ł���Ƃ����_�ł��B
�@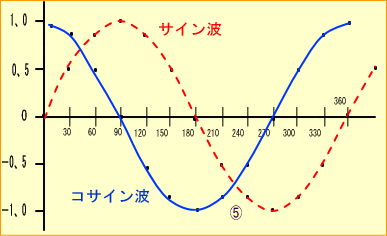
�@�������A���̒��O�ɂ������Ă���@�@�i�P�^�Q�j �@�̓R�T�C���g�S�̂��Q�Ŋ��邱�Ƃł��B�}�C�i�X�����͌�ŏ������܂��B
�@�܂�`�E�������Q���������̏ꍇ�ōl����ƁA�`�ɑ������鐔�l���P�^�Q���O�C�T�ɂȂ��Ă��邱�Ƃ��Ӗ����܂��B
�@����Ĕg�̐U�ꕝ�����̔g�̔����́@�O,�T�@�ɂȂ�킯�ł��B
�@����Ɂu�Q�������v�́u�Q���v�Ƃ͎��g�������Q�{�ɂȂ������Ƃ�\���܂��̂ŁA�g�̕ω����{�̑����ɂȂ�܂��B
�@�ł������A���g�����Q�{�́@�������Q���@�Q�@�@�� �� ���@�@�Ƃ����g�i�̎����j�ł́A�������g�i�Ԃ̓_���j�̔��������ŁA���łɂP�������I���܂��B
�@����@�@�|�i�P�^�Q�j �@�͑O�Ƀ}�C�i�X�̋L�������Ă���̂ŁA�g�`�̓v���X�}�C�i�X�t�ɂȂ�A�܂�G�𗠕Ԃ�(���])���Ă������̂ł��B
�@�d�グ�Ƃ��āA��ɂ����@�@�{�i�P�^�Q�j�@�@������̂ŁA�S�̂��O�C�T������Ɉړ������āA���S�����O�C�T�ɂ��܂��B
�@����ł���Ɠd�͂������g�`���o���܂����B
�@�������A���̊G�̏c���͓d���ł͂Ȃ��A�|���Z�̓����Ȃ̂œd�͂v�i���b�g�j��\���Ă��܂��B
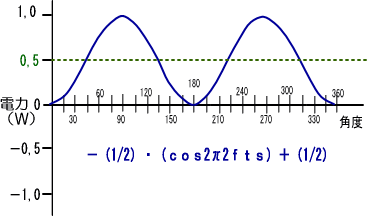
���̎��u�R�v�̔��������́A�u�J�v�܂蔼�����牺�Ɠ����`�Ȃ̂ŁA���̕���������ĒJ�̒��ւ����ۂ����Ă��܂��܂��B
����ƁA���傤�ǁ@�O,�T�@�̂Ƃ���ŕ���ɂȂ�܂�
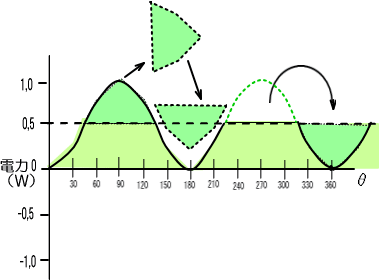
���̂悤�Ɂ@�s�[�N�P�u�@�̐����g�d���ƁA�s�[�N�P�`�@�̐����g�d�����������킹�������g�d�͂́A
�@����ɂȂ炷�Ɓ@�O,�T�v�@�ɂȂ��Ă��܂��܂����B
����Ȃ�t�Ɂ@�O,�T���i�P�^�Q�j�@�̕����������߂�A���ۂɗL���ȓd���Ɠd�����v�Z���邱�Ƃ��ł���킯�ł��B����ƁA
�d���́�O,�T����i�P�^�Q�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@����P�^��Q
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@����Q�^�Q
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���O,�V�i�u�j
���l���d���́�O,�T���O,�V�i�`�j
�@�܂��V�O�p�[�Z���g�����Ȃ��������ƂȂ�܂����A����ł���ƒ����ƌ�����ׂ���]���A�܂�����l�ƂȂ�܂����B
�@���͉ƒ�̃R���Z���g����o�Ă���d���́A���łɎ����l�łP�O�O�{���g�ł��B�����Ńs�[�N�Ȃ牽�{���g�o�Ă��邩�v�Z���Ă݂�ƁA
�@�@�@�@�@�P�O�O�u�������l���s�[�N�l�~�O,�V
�@�@�@�@�@�@�@�@�@�@�@�s�[�N�l���P�O�O�u���O,�V
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���P�S�O�u�@�@�@�@�@�@�@�@���̓d���Ŏ������͊��d���܂��B
�d�����[�^�Ȃǂ̕\���́A�قƂ�ǂ������l�ŕ\����܂��̂ŁA�s�[�N�l��m�肽�����̓��[�^�̒l���P��S�{�A�����ɂ́�Q�{���Ȃ���Ȃ�܂���B
�@�@�@�y�X�z�R���f���T�ƃR�C���Ƃ�����\�I�ȕ��i
�`�j�@�R���f���T
�R���f���T�͓��{��ł́u�~�d��v�Ƃ����܂��B�[�d�ł���^�C�v�̓d�r�A�u�~�d�r�v�Ɏ��Ă��܂����A�d�C�̒��ߕ����Ⴂ�܂��B
�d�r��~�d�r�͓d�C�����w�ω��ɂ��A�����Ƃ��̃C�I���Ƃ����ʂ̌`�ɂ��āA���߂Ă��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@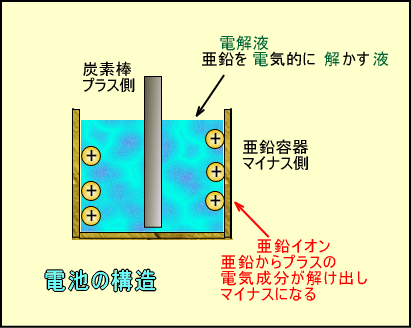
�����č��̔_�ƂɗႦ��ƁA�Ă������ݕ��ƌ������Ď����Ă����ԂŁA���[�ꏊ�ɂ͍���܂��A�ĂѕĂɖ߂��ɂ͎��Ԃ�������܂��B
�����������ݕ��ł�����A���R���Ăɕς��邱�Ƃ��ł��܂��B
����ɑ��R���f���T�́A�d�C�̂܂ܒ~���܂��B�_�Ƃ̗�ł����A���Ă̂܂����Ă��邽�߁A�傫�ȑq�ɂ��K�v�ł��B
�@���������Ă��̂��̂ł�����A�ȒP�ɔ��~���ȒP�ɕ��o���邱�Ƃ��ł��܂��B
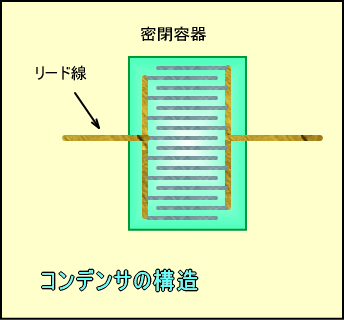
�R���f���T�̍\���͂������ĊȒP�ŁA�Q���̋����̔��킸���Ȍ��Ԃ������Č��������킹�ɗ��Ă���o���オ��܂��
�������������m���G�ꍇ��Ȃ��悤�A�킸���Ȍ��Ԃ�������̂͑�ςȂ̂ŁA�ԂɎ��┖���t�B�������͂��݂܂��B
�͂��ލޗ��ŃR���f���T�̖��O���y�[�p�[�R���f���T�Ƃ��t�B�����R���f���T�ȂǂƂ����܂����A�Ȃɂ��͂��܂���C���g�����Ƃ�����܂��B�@

�܂������̔̂܂܂ł͏ꏊ���Ƃ�̂ŁA�����A���~�z�C���̂悤�Ȃ��̂ŃT���h�C�b�`�\��������A��������邮�銪���č��グ�܂��B
�T�O�O�~�ʂQ���̊ԂɂP���~�D�P��������ł��A����ςȃR���f���T�ł����l�i�͂P���P��~�Ɗ����ł��B
����ȊȒP�ȍ\���łȂ��d�C�߂���̂ł��傤���B
�܂��v���X�`�b�N�̉��~���̗�������ǂȂǂ��g���Ă��̎��̕����ӂ肻�����܂��B
����Ǝ��̃v���X���ƃ}�C�i�X���������������~���ɂ������Ă��܂��܂��B
����ʼn��~���Ɏ��߂鎖���o�����ƌ������ƂɂȂ�܂��B
���������ۂ̎��͂P�̒��Ƀv���X�ƃ}�C�i�X�̗����������Ă���̂ŁA�ӂ肻�����ǂ��납�A
�@���̑O����u���v�̂悤�ɂ������Ă��܂��A�����ł��܂���B
�@�@�@�@�@�@�@�@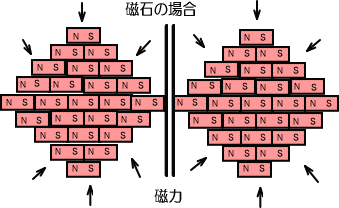
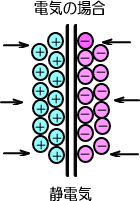
����d�C�̏ꍇ�́A�v���X�ƃ}�C�i�X���������蕪����A���݂��Ɉ����������͂̑���ɁA�Ód�C�ƌ����͂������Ă��܂��B
�����Ō��Ԃ��͂��ނQ���̋����̔ɓd�C��Ód�C�̗͂ł��߂���̂ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�������m�̌��Ԃ́A�����ق����Ód�C�̗͂������Ȃ邽�ߍD�܂����̂ł����A���H������Ȃ�܂��B
�܂��A�����d����������ƌ��Ԃ̐≏�̂�d�C���˂������āA���d���₷���Ȃ�܂��B
����A�����̖̔ʐς��傫���قǒ��߂���d�C�̗ʂ������܂��B
�@�@�@�@�@�@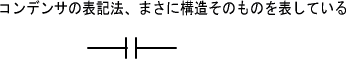 �@
�@
�a�j�@�R�C��
�d���͓d�C�𗬂����߂̒ʂ蓹�ł����A�P�{�̓d���ɓd�C�����ꂽ�����łƂĂ��ア�d���ɂȂ��Ă��܂��B
�����d���ɂ������Ȃ�Γd�������{������悤�Ɍ�����H�v������Ηǂ��A�ӂ��͂��邮�鉽����d���������܂��B
������R�C���ƌ����܂����A����Ɏ��C�͓S�Ȃǂ̂ق�������₷���̂ŁA�S�c�����܂��B
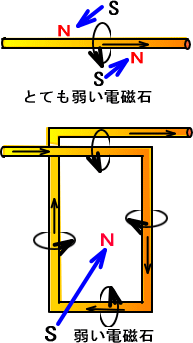 �@�@
�@�@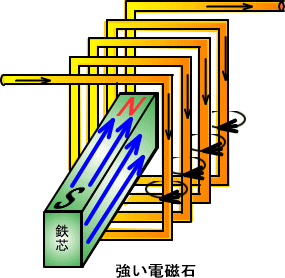
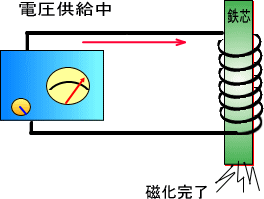
�d���͓d����S�c�Ɋ����������̃R�C���ł����A�d���������ǂ������ƁA�����ʂ̎d�������܂��B
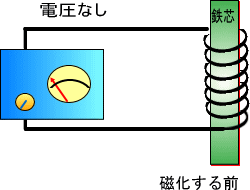
�@�@�ʏ�S�c�͓������E�̕������o���o���ŁA���̐����͋N����܂���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@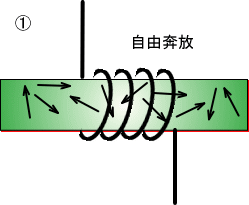
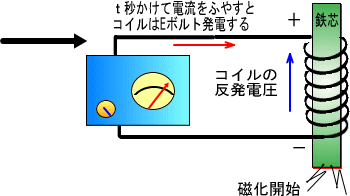
�������d�r���R�C���ɂȂ���ƁA�������E�̕��������낢�A���̐������N����܂��B
�@�܂�R�C���ƓS�c�œd�͂����͂ɕω����܂��B
�@����ł����Ȃǂ��Ђ��������グ����A�d�r���͂����Ƃ����������āA���ł͂Ȃ��Ȃ������Ƃ�������܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@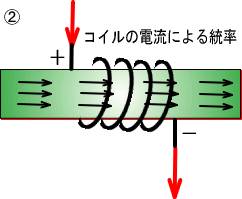
�@�Ȃ���̎��A�d�͂���ω����Ă������͂́A�ǂ��֍s�����̂ł��傤���B
���͍Ăѓd�C�ɂȂ��ăR�C���ɖ߂��Ă����̂ł��B�R�C���ɓd��������Ȃ��Ȃ�����A�S�c�����ɖ߂����Ƃ������Ƃ́A
�@�S�c�̋C�����̒��Łu���̓C�����I���Ƃ̕��ʂ̓S�ɖ߂肽���B�v�Ƃ����͂�����������ł��B
�S�̓X�v�����O�ɑ�\�����悤�ɁA���C�����łȂ��@�B�I�ɂ��A���ɖ߂낤�Ƃ��鋭�łȐ��i������悤�ŁA�u�S�l�v�Ȃǂƌ������t������܂��B
���̌��ʂm�ɂ͂m�����炤�A���`�m�ɁA�܂�r�̗͂��N�����̂Ɠ����悤�ɂȂ�܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@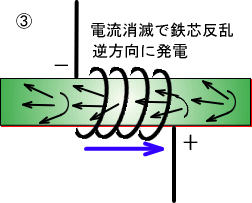
�r�ɂ������A���`�r�ƂȂ�A�܂�Ŏ����R�C���̒��łЂ�����Ԃ����悤�ɂȂ������ʁA�R�C���ɂ͋t�̌����ɓd�C���N����܂��B
���̌ケ�̓d�C�̓R�C���ƓS�c�̊ԂŁA���C�ɂȂ�����d�C�ɂȂ�������J��Ԃ��Ȃ���A�M�G�l���M�[�ɂȂ��ăR�C�������߁A�₪�ď����Ă��܂��܂��B
�@���̂悤�ɃR�C���͏u�ԓI�ɓd�������Ƃ����`�ŁA�d�C�߁A�d�����S�ɖ߂�͂Ŕ��d���Ă��邱�ƂɂȂ�܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@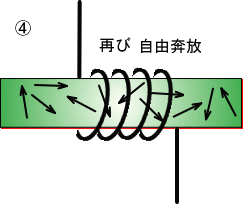
�@�ł�����A�����S�c�����ɖ߂炸�i�v���ɂȂ��Ă��܂�����A�R�C���ɂ͓d��������܂���B
�R�C������������d�C�߂邽�߂ɂ́A�傫�ȓS�c���K�v�ł����A�����d�����ׂ��ƁA�������������A�d���̓d�C��R�������Ė��ʂ������Ȃ�܂��B
�Ƃ���łP�O�O����d���������͖̂ʓ|�Ȃ̂ŁA�P�O�O�{���˂��d�����P����������ǂ��ł��傤�B
�c�O�Ȃ��炻�̎��́A�e�X�̓d���ɗ����d�����P�O�O���̂P�ɂȂ��Ă��܂��A�d���͂P�O�O�{�����Ă����Ă��A�P�����̂Ɠ����ɂȂ�܂��B
�܂芪���d���̑������P�O�O�{�ɂȂ��������A�Ƃ������ł��B
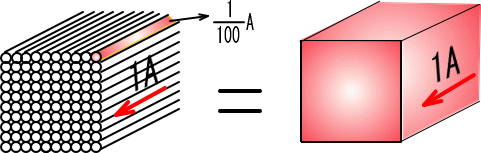
�@������̎��A�d�����P�O�O�{�ɂ���P�O�O�����̂Ɠ����ł��B
�@�������R�C���ɂȂ���d���܂ő����������Ȃ��ƁA�d���̓d�C��R���傫���Ȃ��Ď��p�ɂȂ�Ȃ����߁A�ʏ킻�̂悤�Ȏ��͍s�Ȃ��܂���B
�R���f���T�͓d�C�߂鎞�ƕ��o���鎞�̃v���X�}�C�i�X�����������ł��B
����ɔ�ׁA�R�C���͕��o���鎞�A�t�����ɂȂ��Ă���Ƃ������҂̑������鐫�����A���ɂ��܂��@�\�������ēd�C�̐��E���������Â���܂��B
�@�����������Ƃ������l�X�̈̋Ƃ��f���炵���̂ł����A���ꂪ�p�ӂ���Ă����F���ɂ͊���������܂���B
�@�@�@�y�P�O�z�R���f���T�̖���
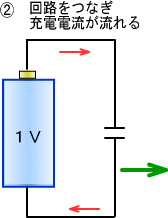
�d�r�ɃR���f���T���Ȃ��ł��Q���̌��Ԃ̊J���������Ƃ��������ł�����d���͂Ȃ���܂���B
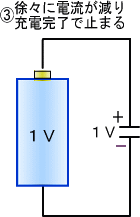
�������ŏ��̈�u�����̓R���f���T���[�d���邽�߂̓d��������܂��B
�[�d���I��ƃR���f���T�̗��[�͓d�r�Ɠ����d���ɂȂ�A�d�r�������ЂƂ������ɐڑ����ꂽ�悤�ɂȂ��āA�d�C�̗���͎~�܂�܂��B
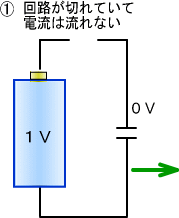 �@
�@ �@
�@ �@
�@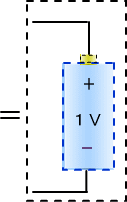
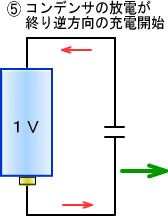
�����œd�r���v���X�}�C�i�X�t�ɂȂ��ł݂�Ɠd�r�̃v���X�ɃR���f���T�̃}�C�i�X���Ȃ���A�R���f���T�̃v���X���d�r�̃}�C�i�X�ɂȂ���܂��B
����͓d�r���Q����ɐςݏグ�āA��̓d�r�̃v���X�Ɖ��̓d�r�̃}�C�i�X���V���[�g�������̂Ɠ����ɂȂ�܂��B
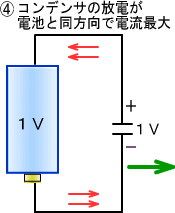 �@
�@ �@
�@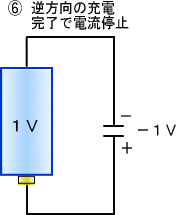
�d�r���Q����ɂ�����ł̃V���[�g�Ȃ̂ŁA�ŏ��d���͐����ǂ�����܂����A���炭����ƃR���f���T�̓d�C�͕��d���I���܂��B
���̌�R���f���T�ɑ��t�����̏[�d���n�܂�A���x�͂Q�̓d�r���������܂ɕ���ڑ����ꂽ�悤�ɂȂ�̂ŁA�d�C�̗���͍ēx�~�܂�܂��B
�d���̌�������シ��̂͌𗬂ł�����A�R���f���T�͂��̂悤�ȏ[�d�ƕ��d���J��Ԃ��A�ԐړI�Ɍ𗬂𗬂��Ă��邱�ƂɂȂ�܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@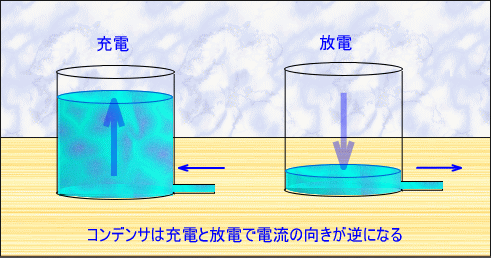
�[�d�Ƌt�����ɕ��d���J�n����B�����͗������𗬂������ԐړI�ɗ����B���ꂪ�R���f���T�̖����ł��B
�R���f���T���Ód�C�ŏ[�d�ł���d�C�̗ʂ�Ód�e�ʂƌ����܂��B
�@�@�@�y�P�P�z�R�C���̖���
�R�C���͓S�c�ɓd���������������̂��̂ł�����A�d�r���Ȃ��ƒ���������d�����ł��܂��B
���̎��A�R�C���͓d���ɒ�R���Ȃ�����d���ɂ���Ă��܂��܂��B
�d���ɒ�R����Ƃ́A��R���傫���Ȃ����ƌ������ł����A�ʂ̌���������ƁA�R�C���ɋt�����̓d�����������āA
�@�O�����炫���d����ł������Ă���Ƃ��l�����܂��B
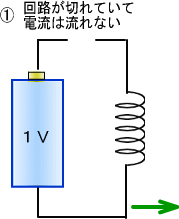
�����x�̋����̓d�����ł���ƁA�R�C���͓d���ɋt�炤�̂��~�߂܂��B
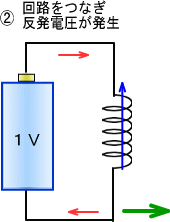
�����Ȃ�Ɠd����W����̂̓R�C���̒�����R�����ɂȂ�A�d���͍ő�ɂȂ�܂��B
 �@
�@ �@
�@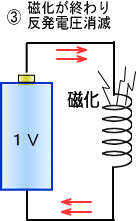
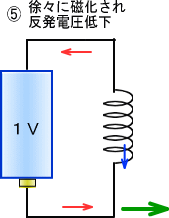
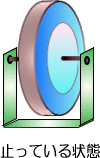
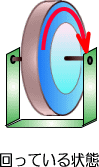
�@����Ǝ����X�^�C���ŃG�l���M�[��~������̂ɁA�t���C�z�C�[���i�͂��ݎԁj������܂��B
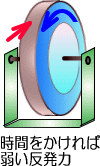
�@�Î~�����t���C�z�C�[���ɊO�������͂�^����ƁA�ŏ��t���C�z�C�[���͊����̖@������A�Î~��Ԃ���낤�Ƃ��āA
�@�������㔽�������]�͂��������܂����A�₪�Ă���͌�������]���n�܂�܂��B
���̂悤�ɂ��Đ����͉͂�]�͂Ƃ��ē����ɒ~�����A�O����]�͂������Ȃ�ƁA���x�͒~����ꂽ��]�͂��g���A
�@�ꂽ���Ɠ�������ɐ����͂��ł��邱�ƂɂȂ�܂��B
�@�������������d���̌����̈Ⴂ���A�R���f���T�ƃR�C���Ƃ̈Ⴂ�ł��B
�@�@�@�@�@�@�@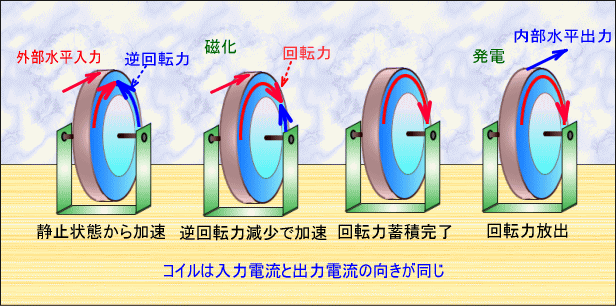
�R�C���ɘb��߂��āA�d�r���͂����Ă݂�ƓS�c�����ɖ߂낤�Ƃ��邽�߁A�������ꂽ���Ɠ�������ɔ��d���܂��B
���̌�d�r���t�����ɂȂ���Ƃǂ���̓d�����t�����ɂȂ��Ă���̂œd�r�̃v���X�ǂ������Ȃ�������ڑ��̂悤�ȏ�ԂɂȂ�A
�@���̏u�Ԃ͓d��������܂���B
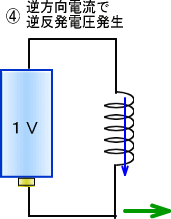
�������A���炭����Ƌt�����̓d�r�ƁA�������t�����̃R�C�������d�����d���ɂ���āA���x��Ĕ����d�����������Ȃ���A
�@�t�����Ɏ����d��������܂��B
 �@
�@ �@
�@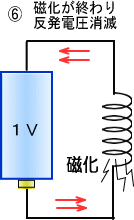
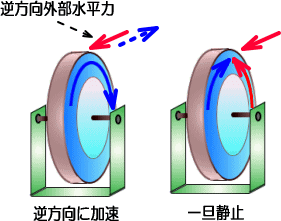
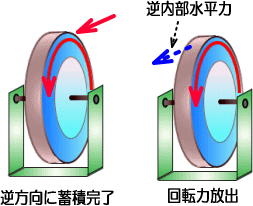
�@��]���̃t���C�z�C�[���ł����Ε�������O����]�͂������ƁA�����u���[�L�ƂȂ�A������������t��]�͂��������܂��B
�@�������O����]�͂�����������ƁA�t��]�͂��������Ă䂫�A�Î~��Ԃ��o�Ĕ��Ε����̉�]�͂��~������̂ł��B
 �@�@
�@�@
�@�R�C���͂����ɗ����d���œd�������Ȃ���~�d���A�d��������ΓS�̖߂�͂ŁA���܂łƓ���d�������ɔ��d����B
�@�����͒ʂ����𗬂͒ʂ��ɂ����B���ꂪ�R�C���̖����ł��B
�@�܂��R�C���̌𗬂ɑ����R�����ȃC���_�N�^���X�ƌ����܂��B
�R�C���̋L���@�@![]()
�Ƃ���ŁA���̓S�c�ɂ����ЂƂʂ̃R�C������������ǂ��Ȃ�ł��傤���B
�S�c�͗����̃R�C���ɑ����ʂ����Ȃ��̂ŁA�Q�̃R�C���ɋt�����̓d�C�����o����܂��B
�@���̂悤�ɃR�C���͓S�c����āA�ʂ̃R�C���ɓd�C�𑗂����������A������g�����X�Ƃ����܂��B
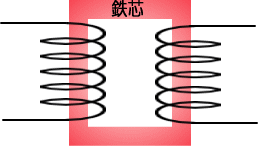
�i�g�����X�j
�A���d�����ω����Ȃ��ƁA�S�c�����͂߂���f���o�����肵�Ă���Ȃ��̂ŁA�d���̕ω��̖��������͑���܂���B
�g�����X�ɂ��Ă͌�قǏڂ������ׂ܂��傤�B
�@�@�@�y�P�Q�z�R���f���T�ƃR�C���ƌ��@�@
�R���f���T�ƃR�C���͌𗬂ɑ��Ĕ��̐��i�������Ă��������ƕ������Ă��܂������A�����������m�ɂ���ɂ́A
�@�Ód�e�ʂ⎩�ȃC���_�N�^���X�̒l�ƁA���g���Ƃ̊W�ׂ�K�v������܂��B
���g���́u�P�b�ԁv�̐U���A�R���f���T�͓d�C�̒��܂�u���ԁv�A�R�C���͓d�������d����u���ԁv�����ʂ̃q���g�ɂȂ肻���ł��B
����ɃR���f���T�͐Ód�e�ʂƂ����ɒ��܂��Ă���u�d���v�ŁA�~�����d�C�̗ʂ����܂�̂ɑ��A
�@�R�C���ł͎��ȃC���_�N�^���X�Ƃ����ɗ����u�d���v�ŁA�~�����d�C�̗ʂ����܂�܂��B
�`�j�d���f�q�ł���R���f���T�ƌ𗬒�R
�P�A���y�A�̓d�����P�b�ԗ��ꂽ�Ƃ����ꂽ�d�C�̗ʂ��P�N�[�����̓d�ׂƂ����܂��
�P�N�[�������P�`�~�P�r
�d�����uI�v�A���Ԃ��u���v�A�d�C�̗ʁA�d�ׂ��uQ�v�ƒu�������Ċ|���Z�ł���킷��
Q��I�~��
���̓d�C���P�t�@���b�h�Ƃ�����ʐς��������܂�P�t�@���b�h�̃R���f���T�ɒ��߂�ƁA�d�����P�{���g�ɂȂ�܂��B
�d�������ʁA�Ód�e�ʂ������̒�ʐρA�d�C�ʂ����܂������ʂƂ���ƁA���ʂ͒�ʐςƐ��ʂ̊|���Z�Ōv�Z�ł��܂��B�����d�C�ɒ����ƁA
Q��C�~E
�Ə����܂��B�����łp�̏o�Ă����Q�̊|���Z���P�ɕ��ׂ��
Q��I����CE�@
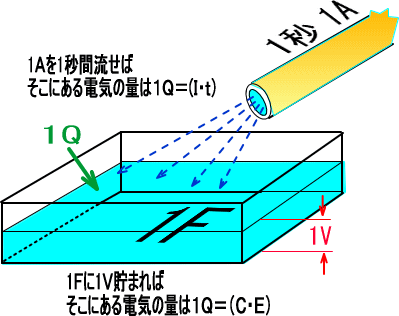
�ƂȂ�܂����A���̎����@It��CE�@�̂Ƃ����ό`���Ă݂��
���^C��E�^I�@
�@
����I�[���̖@�����v���o���ƁA���̎��̉E��
E�^I��R�i��R�j�@�ł��̂Ł@
�@�@�@�@�@���^C��E�^I��R
�@�@�@�@
�ƂȂ�܂��B����̓R���f���T�̎��𗬒�R�Ȃ̂ł��傤���B�Ƃ肠���������̒�R�q�Ƌ�ʂ��邽�߁A
�𗬂̒�R���uX�v�ƒu�������Ă݂��
�@�@
���^C��X
���̎��̈Ӗ����l���Ă݂܂��傤�B�@X�@�͂����炭�R���f���T�@C�@�̌𗬒�R�ł��B
�����ō����̕���@C�@�܂�Ód�e�ʂ𑝂₷�Ɓ@X�@�͏������Ȃ�܂��B
���q�u���v�͎��ԂŁA���ꂪ�傫���Ȃ�Ƃ������͂������[���d����A�܂�g�̓������x���Ƃ������ƂɂȂ肻���ł��B
�ȏ�̂��Ƃ���A�R���f���T�͌𗬂ɑ�
| �@�@�@�@�������g���Ȃ�Ód�e�ʂ��傫���قǒ�R��������B �@�@�A�@�����Ód�e�ʂȂ���g���������قǒ�R��������B |
�Ƃ������Ƃ��\���ł��܂��B
|
|
|
|
|
|
|
|
|
|
|
|
�Ƃ���łp���b�d�Ƃ������ŁA�d�ׂp�����̗ʁA�b���e��̒�ʐρA�d���d�����̒��܂��������Ɏ��Ă���Ə����܂����B
���ێ����ǂȂǒ�ʐς̏������e������Ă��������A���~�Ɉڂ�������ƁA���̗ʂ͓����ł��A���ʂ������ƒႭ�Ȃ�܂��B

����R���f���T�ɂ����Ă������悤�Ȏ����N���܂��B
���̓d�C�����܂��Ă���R���f���T�̓d�ɊԂ𗣂�����A�d�ɂ̖ʐς����炵���肵�ĐÓd�e�ʂ����炷�ƁA
�@���ꂾ���œd�ɊԂ̓d���͍����Ȃ�܂��B
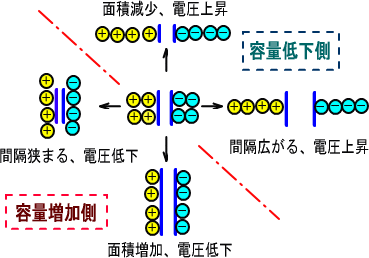
�_�͐Ód�C��ттĂ��܂����A��ʂ̉_���Ă̓������ŋ}�㏸����ƁA�����P�̓d�ɂł����n�ɑ��A
�@�ɂ߂č����d���ɕω����邽�߁A���ɂ͗������܂��B
�@�@�܂����������_�́A�Ⴂ�ʒu�̉_�ɑ��Ă����d�������邽�߁A�_���m���������N���Ă��܂��B
�a�j�d���f�q�ł���R�C���ƌ𗬒�R
�R�C���ƃR���f���T�̂����݂ň�ԈႤ�Ƃ���́A�R���f���T���d�C��d�C�̂܂[�d���Ă���̂ɑ��A�R�C�����d�C�����C�ɕϊ����Ē~�d���Ă���_�ł��B
�@�܂�d�C��ÓI�ɓd�ׂ̗ʂƂ��Ē��߂�̂ł͂Ȃ��A�d�ׂ̗����^���G�l���M�[�����C�G�l���M�[�Ƃ��Ē��߂Ă���Ƃ����܂��B
�@�ł�����R���f���T�ȏ�ɁA�𗬐�p�̃_�C�i�~�b�N�ȑf�q�Ƃ������Ƃ��ł��܂��B
���̋������E�F�[�o�[�iWb�j�ƌ����P�ʂŕ\���܂����A����R�C���ɁA�d�����P�A���y�A�����ĂPWb�@�̓d�����o�������A
�@���̃R�C���̎����ȃC���_�N�^���X�͂PH�i�w�����[�j���ƌ����܂��B�����ł��̊W�����ɂ����
Wb��L�~I
�@�ƂȂ�܂��B���̎��́A�PH�̃R�C���ɂP�`�̓d���������PWb�@�̎��ɂȂ邪�A�Q�`�ł͂QWb�@�̎��ɂȂ邱�Ƃ������Ă��܂��B
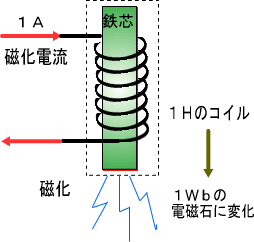
�������Ăł����PWb�@�̓d���́A�d�����ƁA�t�����ɓd�������܂����A���ۂ͓d������������Ɠd���Ɍ������ēd�������A
�@�d���̌������͋t�����ɔ��d���܂��B
�����Ă��̓d���́A�d�����ω����鎞�ԁ@���@�b�̒����ɂ���Ă��ς��܂��B
�Ⴆ�Γd�����ω��o���钼���d����p���A�d�����������㏸������ƒႢ�d�����A�܂������㏸��������d�����������܂��B
 �@
�@
 �@�@�@�@�@�@�@
�@�@�@�@�@�@�@ �@�@�@�@
�@�@�@�@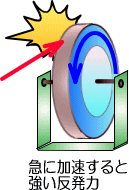
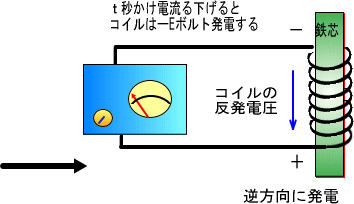
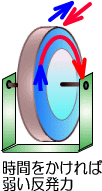
�@���̌�A�d����������茸��������ƒႢ�d�����A�܂��}�Ɍ���������ƍ����d�������܂łƋt�����ɔ������܂��B
�@�d����ؒf���Ă������ŁA�ؒf�������ɍ����d�����������āA���d���N�������Ƃ�����܂��B
 �@
�@
 �@�@�@�@�@�@
�@�@�@�@�@�@ �@�@�@�@�@�@
�@�@�@�@�@�@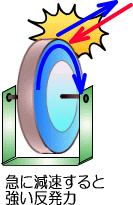
�����œd������������Ƃ��t�����ɔ��������d�����u�|E�v�ɁA���Ԃ��u���v�ɒu�������Ď��́uWb�v�Ƃ̊W���|���Z�ł���킷�ƁA
Wb���|E�~��
�@�ƂȂ�܂��B�v���ɊW����Q�̊|���Z����ׂ��킹��ƁA
Wb���|E����LI
�@�ƂȂ�܂������̎��̒��Ł@�|E����LI
�|L�^����E�^I��R
�@�����łq���𗬂̒�RX�ɒu�������ĕ\�L����Ɓ@
X���|L�^��
�@X�͂����炭�R�C���k�̌𗬂̒�R�l�ł��傤�B�ŏ��Ƀ}�C�i�X�̋L�����t���Ă��܂����A�𗬂͂��Ƃ��Ƃ��v���X�ɂȂ�����}�C�i�X�ɂȂ����肵�܂��B
�@�����ŃR�C���̌𗬂ɑ��鐫�������ׂ邽�߂ɁA�}�C�i�X�̋L�����ꎞ���������
�@�@�@�@�@�@�@�@�@�@�@X��L�^���@�ƂȂ�܂��B
���̎��̈Ӗ����l���Ă݂܂��傤�B����̎��Ԃ��������Ȃ�Ƃ����͓̂d���̓������Z���Ԃő����ω�����A�܂���g���������Ȃ�炵�����Ƃ������܂��B
�܂����q�̓C���_�N�^���X�̒l���̂��̂ł��B�ȏ�̂��Ƃ���R�C���͌𗬂ɑ���
| �@ �@�@�@ �@�����C���_�N�^���X�Ȃ���g���������قǒ�R��������B �@ �@�@�A �@�������g���Ȃ�C���_�N�^���X���傫���قǒ�R��������B �@ |
�Ƃ����A�R���f���T�Ƃ͂܂������t�̐����������Ă��邱�Ƃ��\���o���܂����B
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
�@�@�@�y�P�R�z�𗬒�R�Ɠd���̎��ԍ�
�`�j�d���f�q�ł���R���f���T�̓d��
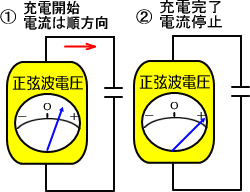
�d�r���R���f���T�ɂȂ��ƁA�܂��[�d����d��������A�@�@�d�r���Q�ɂȂ����悤�ɂȂ�܂��B�A
�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@
�@�@�@�@�@�@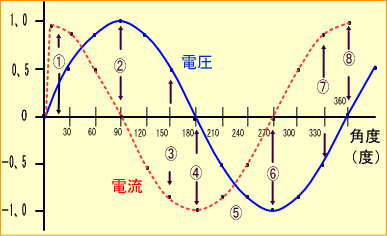
�����ʼn����̗��R�ɂ��A�d�r�̓d��������Ɍ����čs���Ɓ@�A�@���x�̓R���f���T�̓d���̕����d�r�̓d����荂���̂ŁA
�@�d���̓R���f���T����d�r�̂ق��t�����܂��B
�@���̏�Ԃ������Ă݂�ƁA�d�r�̃v���X�}�C�i�X���t�����ɂȂ�O�ɁA���łɋt�����̓d�����A�R���f���T�̕��d�ɂ���ēd�r�Ɍ������ė���Ă������ɂȂ�܂��B
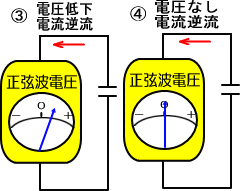
�@�����g�̓d�����R���f���T�̓d�����Ⴍ�Ȃ�n�߂�̂́A�ŏ��̎R�̒��シ�Ȃ킿�X�O�����߂���������ł����A�����ɓd���̓}�C�i�X�������n�߂܂��B�A�`�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@
�@�@�@�@�@�@
�����g�d���̐��l���}�C�i�X�ɂȂ�̂͂P�W�O�����߂��Ă���Ȃ̂ɁA�d�����X�O���ɂȂ������_�ł���ɓd���̕��̓}�C�i�X�ɂȂ�n�߂Ă��܂��B�C
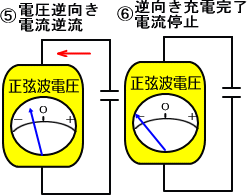
�@���̂悤�ɁA�R���f���T�ɗ����𗬓d���́A�d���̃v���X�}�C�i�X�̋t�]���ꌩ�i��ŗ���Ă���悤�Ɍ�����̂ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@
�@�@�@�@
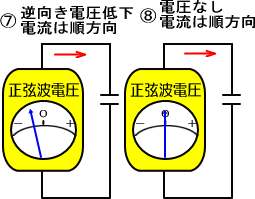
�����œd���ɑ��R���f���T�ł͓d�����d�����X�O����ɐi��ł���̂ł͂Ȃ����ƍl�����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@
�@�@�@
�@�@�@�@�@�i�@�����G�ւƐi�݁A���̌���A�֖߂�B�j
�a�j�d���f�q�ł���R�C���̓d��
�R�C���̓R���f���T�ƈႢ���[�̓d���ł͂Ȃ��A�ǂ�قǃR�C���ɓd�������ꂽ���ɂ���āA�~�����d�C�̗ʂ����܂�̂ŁA�d���𒆐S�ɍl���܂��B
�����Ă��̎��ɃR�C���̗��[�ɔ��������d�����A���̓R�C���Ɋ|�����Ă���d�����̂��̂ɂȂ�܂��B
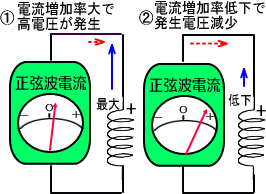
�܂��R�C���ɓd���𗬂����Ƃ���ƁA�����d�����������܂��B�������d���̑��������₩�ɂȂ�ƁA��������d�������X�ɒቺ���܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@
�@�@�@�@�@�@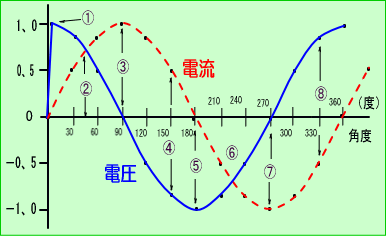
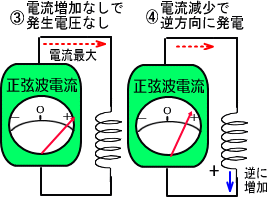
����ɓd���̑������~�܂�ƍ��x�͋t�����̓d�����������ēd���̓}�C�i�X�ɂȂ��Ă��܂��܂��B
�T�C���g�Œl���}�C�i�X�ɂȂ�̂͂P�W�O�x�̎��ł����A�d���̑������~�܂�X�O�x�̎��_�ł���ɓd���̓}�C�i�X�ɂȂ��Ă��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@
�@�@�@�@�@�@
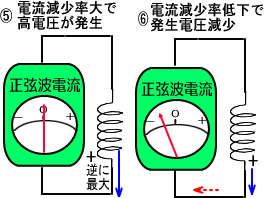
�@�����̎�����R�C���̓d���͓d�����X�O�x��ɐi��ł���̂ł͂Ȃ����Ɨ\���ł��鎖�ɂȂ�܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@
�@�@�@�@�@�@�@
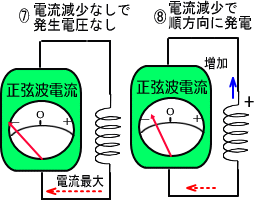
�@�A���R���f���T�̎��͓d���̐����g����ɍl�����̂ŁA���l�̌�����������A�d���ɑ��R�C���̓d���͂X�O�x�x��Ă���A
�@������܂��R���f���T�Ƃ͑Ώ̓I�Ȑ��i�炵���Ƃ킩��܂���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@
�@�@�@�@�@�@�@
���̂悤�ɓd���Ɠd���̔g�`�̊p�x���X�O�x����Ă��鎖���A�u�ʑ����X�O�x�����v�Ƃ��u�ʑ������X�O�x����v�Ȃǂƌ����܂��B
�@�@�@�y�P�S�z�ʑ����̂��鐳���g�𐔎��ƋL���ŏ���
�����g���P�ԊȒP�Ȍ`�ŏ����Ɓ@�r�������ł��B���Ƃ����_���O�x����R�U�O�x�܂ňړ��������A���̒l���r�����̌�ɓ���ĎO�p���\��������̎��́A�g�̍����i�}�C�i�X�̎�������j�����@�@����܂��B
�����ŁA�ʑ���������Ƃ�����Ƃ��āA�X�O�x�x��Ă���g�`��`���Ă݂܂��傤�B
�܂����ꂩ��́u�x�v�̒P�ʂ͐����Ƃ̑�������u���v�̋L���𑽗p�������Ǝv���܂��B
�X�^�[�g�͂X�O������ł��B���̂Ƃ������̒l�͂X�O���Ȃ̂ł��̂܂܂ł͂r�����X�O���̒l�܂�P�ɂȂ��Ă��܂��܂��B
�������{�����X�^�[�g�n�_�Ȃ̂œ��R�O�ɂ��Ȃ�������܂���B�����������l���X�O���̎��O�ɂȂ�悤�ɁA�ŏ�������������|�X�O���Ƃ��܂��B
���ɂ����
�������i���\�X�O���j
�@���̂悤�ɂ��Ă����A�����X�O���̎�
�������i�X�O���\�X�O���j���������O��
�ƂȂ��āA�X�^�[�g�̈ʒu�Ƃ��Đ��������l�ɂȂ�܂��B
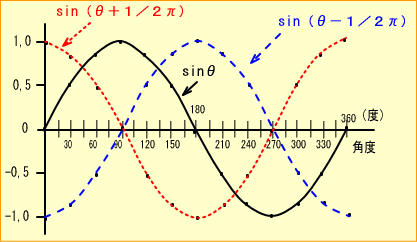
�����łX�O�������^�Q�ł����珑������ς���
�@�@�@�������i���\���^�Q�j�@���X�O���x�ꂽ�����g�ƂȂ�܂��B�t��
�@�@�@�������i���{���^�Q�j�@���X�O���i�����g�ƂȂ�܂��B
�@�@�@�y�P�T�z�𗬒�R�̒l��T���o���肪����
�@�R���f���T�ƃR�C���ƌ𗬂̊W�����낢��킩���Ă����Ƃ���ŁA���悢����ۂ̌𗬒�R�l���Ȃ�Ƃ������o���Ă݂܂��傤�B
�@�h�����b�d�@�Ƃ�������ό`���ďo�Ă����R���f���T�̌𗬒�R��
X�����^C
�@�ƂȂ��Ă��܂������A�u���v�Ƃ������Ԃ̎��̂����Ȃ̂��A����͂����肵�Ă��܂���B�����ł�����x�u���v�̊�{�I�ȈӖ����l���Ă݂܂��傤�B
�܂��P�e�i�t�@���b�h�j�̃R���f���T�ɂP�b�ԓd���𗬂��A�P�u�i�{���g�j�ɂȂ�����A����͂P�`�i�A���y�A�j�̓d��������Ă������ɂȂ�܂��B
���ʂȂ玟�̂P�b����P�u�����ĂQ�u���Ǝv������A�ӊO�ɂ��Q�u�����āA���v�R�u�ɂȂ��Ă����Ƃ�����A���̂P�b�Ԃ͂Q�`����Ă������ƂɂȂ�܂��B
����Ɏ��̂P�b�Ԃł͂����ƌ����āA�Ȃ�ƂO��T�u���������Ă��Ȃ���A���̊Ԃ͂O��T�`����Ă������ƂɂȂ�܂��B
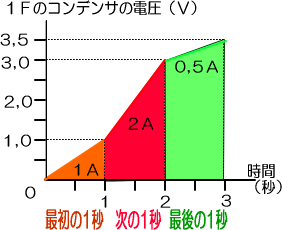
���̎��́A�R���f���T�u�b�v�̒l�����ɂ��āA���ԁu���v�i���̏ꍇ�͂P�b�j���ɓd���̑��������킩��A���ԁu���v���ɃR���f���T�ɗ��ꂱ�d���̗ʂ������邱�Ƃ��Ӗ����Ă���̂ł͂ȁ@���ł��傤���B
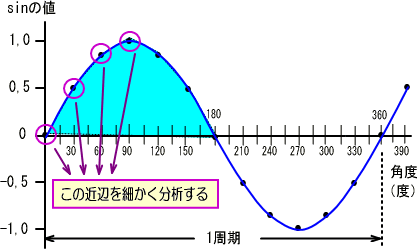
�����Łu���v�̒������A�ǂ̂悤�Ȏ��g���ł������ɑΉ��ł���悤�A�����g�P�����́A�P���ɑ������鎞�Ԃɂ���ƁA
�P�g���ł͂����P�����i�P�^�R�U�O�~�P�j���i�P�^�Q���~�P�j�b
�P���g���ł͂����P�����i�P�^�R�U�O�~�P�O�O�O�j�b���i�P�^�Q���~�P�j�j�b�@
�܂�u���v���@�i�P�^�Q�����j�b�@�ƒu���ǂ̂悤�Ȏ��g���ł��P�g�����P�^�R�U�O�ɕ������ċ�̓I�ȓd���Ɠd���̊W�����ׂ�ꂻ���ł��B
�@�@�@�y�P�U�z�𗬒�R���O�p���\����ׂ����ϑ������@�@
�������ׂ����ϑ�����Ƃ��͌��������g���܂����A�@�������肻���ȓd�C���ۂ́A�v�Z�ŕ��͂��܂��B
�������d�C���ۂ��ׂ������ӏ������ׂ邽�߁A�����悤�ȒP���v�Z�̌J��Ԃ��������Ȃ�܂��B
�`�j�R���f���T�̌𗬒�R
����Ɏg�������g�d���́A�킩��₷���@�P�u�A�P�g���@�Ƃ��܂��B
�@�@�܂��@�u�@�P���v�@�ɂ����鎞�ԁ@�u�@���@�v�@���o�����߁A�P�b���R�U�O�Ŋ����
�����P�b���R�U�O���O��O�O�Q�V�V�W�b�@�ɂȂ�܂�
�@���Ɂ@�P���܂ł��̐����g���i���́A�g���l�@�d�@��
�d���r�����P�����O��O�P�V�S�T�u�@
�@���̗l�q���A�d���Ǝ��Ԃ̊g��}�Ō��Ă݂܂��傤�B
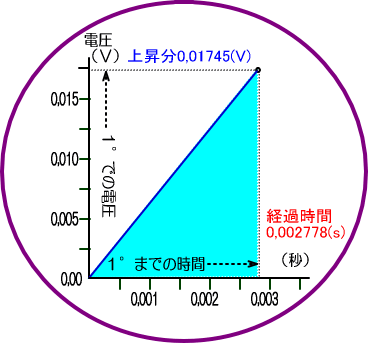
�@�@�@�@�@�@�@�@�@�i�X�^�[�g����P���܂ŃR���f���T�ɂ�����d���Ǝ��Ԃ̊g��}�j
�@����ɃR���f���T�̐Ód�e�ʂb�@���@�b���P�e�@�Ƃ��āA�ȑO�o�Ă����A�R���f���T�̓d�C�I�@�\�@
�@�@�b�E�d���h�E���@�@�����ό`�����@�@�h���b�E�d�^��
�@�Ƃ������ɂ��ꂼ��̒l�������Ɠd���@�u�@�h�@�v�@�̒l��
�@�@�@�@�h���b�d�^�����P�e�~�O��O�P�V�S�T�u���O��O�O�Q�V�V�W�b���U��Q�W�`
���ꂪ�P�u�P�g���̐����g���P�e�̃R���f���T�Ɋ|�������@�O������@�P���܂ł̊Ԃɗ��ꂽ���ɂȂ�̂ŁA
�@�@�O������@�P���܂ł̌𗬒�R���@�@�P�u���U,�Q�W�`���O��P�T�X��
�ƂȂ�܂����A�����P�x�ɂ����鎞�ԁ@�O��O�O�Q�V�V�W�b�@�ł��A�R�O������R�P���̊ԂŊm���߂�ƁA
�@�d���̕ω��́@�O�C�T�u�@����@�O�C�T�P�T�u�@�܂ŁA�܂�@�O,�O�P�T�u�@�ƂȂ�܂��B
�@���̗l�q���A�d���Ǝ��Ԃ̊g��}�Ō��Ă݂܂��傤�B
�@�@�@�@�@�@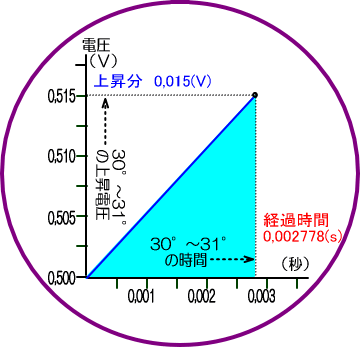
�i�R�O������R�P���܂ŃR���f���T�ɂ�����d���Ǝ��Ԃ̊g��}�j
�@�ł�����d���@�u�@�h�@�v�@��
�@�@�@�@�@�@�h���P�e�~�O,�O�P�T�u���O,�O�O�Q�V�V�W�b���T,�S�`
�@�����Ł@�R�O������@�R�P���̌𗬒�R��
�P�u���T,�S�`���O,�P�W�T��
�@����Ɂ@�U�O������U�P���̊ԂŊm���߂�ƁA�O�C�W�U�U�O�u�@����@�O�C�W�V�U�S�u�@�ɏ㏸���܂��B
�@���̎��̓d�����́@�O,�O�O�W�U�u�@�ƂȂ�A�d���@�u�@�h�@�v�@��
�@�@�h���P�e�~�O,�O�O�W�U�u���O,�O�O�Q�V�V�W�b���R�C�P�O�`
�@�����łU�O������U�P���̌𗬒�R��
�@�@�@�@�@�@�@�P�u���R�C�P�O�`���O,�R�Q�Q��
�Ƒ����܂��B����ɂ��̌���v�Z���Ă݂�ƁA�p�x���i�ނقǓd�������Ȃ��Ȃ�A�W�X������X�O���̊Ԃł́A�O,�O�V�P�X�`�ɂȂ�܂��B
�����ā@�W�X������X�O�@�̒�R�l�́@�P���̎��̖�W�V�{�ɂ�����P�S���ƂȂ�A����ɂX�O���̂Ƃ��͓d������u�@�O�@�ɂȂ�̂ŁA
�@�@�P���ɍl����ƒ�R�l��������Ƃ������ƂɂȂ�܂��B
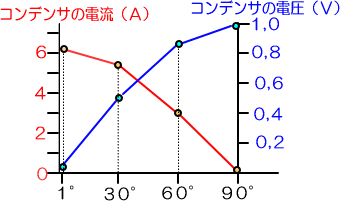
�i�P�e�ɂ�����R���f���T�̓d���ƁA���̏u�Ԃ̓d���̕��͌��ʁj
���̂��Ƃ���P�e�̃R���f���T�̂P�g���ɂ�����𗬒�R�͂P�����̒��ŗl�X�ɕω����Ă��邪�A�ő�Ŗ�����A�ŏ��Ł@�i�P�^�U,�Q�W�j���@�ł��鎖���킩��܂��B
�O���t�Ő����P�x����n�܂��Ă��܂����A�O���̂Ƃ��͂܂��d���������̂ŁA�d���͑��݂��܂���B
���Ȃ݂ɂX�O���ȍ~�̓d���̗l�q�ׂĂ݂�ƁA�d�����X�O���ʑ��̐i�A�ő�U,�Q�W�`�̐����g�ł��邱�Ƃ��킩��܂����B
�����ŃR���f���T�̌𗬒�R�͍ŏ��ɂȂ�@�O������@�P���܂ł̒l���g���܂��B�����Ă��̎��Ԃs�͂P�����̂R�U�O���̂P�ł���@�P�^�Q�����@�ƂȂ�܂��B
�@�@�������Ăw�b��
X�b�����^�b���i�P�^�Q�����j�^�b���P�^�Q�����b
�@�@�ƂȂ�܂��B�����Ɓ@�O���ɋ߂��������ڂ������ׂ邽�߂ɁA���Ԃ��V�Q�O���̂P�b�A�܂�p�x���@�������O,�T���Ƃ��Ă����l�͂قƂ�Ǖς�炸�A
�@�@���p���肪�����Ƃ킩��܂����B
�@�@���̂悤�ɁA���錻�ۂ����ׂ������āA�ω��̓x�������ڂ������ׂ��@�̓j���[�g�����������A�u�����v�ƌ����܂��B
�a�j�R�C���̌𗬒�R
�R�C���ɂ����Ă͐����g�d���ł͂Ȃ��A�P�`�A�P�g���@�̐����g�d�����P�g�̃R�C���ɗ���Ă����ꍇ�ōl���܂��B
�������P���܂ŁA�܂�@�O,�O�O�Q�V�V�W�b��@�̓d���@�h�@�̓R���f���T�̎����l��
�h�@���O��O�P�V�S�T�`
�@�@����ɂ���č����d���̋�����
�P�g�~�O��O�P�V�S�T�`���O��O�P�V�S�T�v��
�܂��P���ɂ����鎞�Ԃ���
�����O��O�O�Q�V�V�W�b
���̎��ԂŔ�������d���d��
�\�d�����k�h
�\�d���k�h�^�����P�g�~�O��O�P�V�S�T�`���O��O�O�Q�V�V�W�b���U��Q�W�u
�@���ꂪ�P�`�����R�C���̗��[�ɂ������Ă���𗬓d���Ȃ̂ŁA�R�C���̌𗬒�R��
�U��Q�W�u���P�`���U��Q�W��
�@�������d���̑����������Ȃ��Ȃ�ɘA��A�𗬒�R�͒ቺ���A�d�����ő�̎��R�C�����[�̓d�����O�u�������Ƃ������Ƃ́A
�@���̎��̌𗬒�R���@�O���@���������ƂɂȂ�܂��B����ăR�C���̌𗬒�R�͍ő�
X�k���k�^�����U��Q�W�i���j
�@�����ā@�ŏ��O���@�̌𗬒�R�������܂��B�܂����Ԃs�̓R���f���T�̂Ƃ��Ɠ��l
�����P�g�^�U��Q�W�����i�P�^�U��Q�W�j�b�@�@�@�@�@�@�@�ƂȂ�܂��B�@
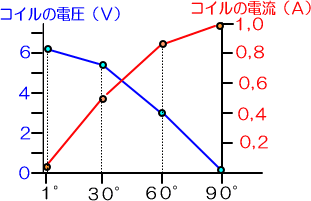
�i�P�e�ɂ�����R�C���̓d���ƁA���̏u�Ԃ̓d���̕��͌��ʁj
�@�ȏ�͂���������g���P�g���̎��̎��ł����A���낢��Ȏ��g���@�u�@���@�v�@�̂P���ɑ������鎞�ԁ@�u�@���@�v�@�@�͏�Ɂ@�P�^�Q�����@�ł�����
�@�@�@�@�k�w�����[�̃C���_�N�^���X�����R�C���́A���g�����ɂ�����𗬒�R�FX�k�͗U�����A�N�^���X�Ƃ���
X�k���k�^�����Q�����k
�@�@�A�@�b�t�@���b�h�̐Ód�e�ʂ����R���f���T�́A���g�����ɂ�����𗬒�R�FX�b�͗e�ʃ��A�N�^���X�Ƃ���
X�b�����^�b���P�^�Q�����b
�@�ƂȂ�܂����B�P�^�Q���@�����Ԃ̎����������Ă���̂́A�������^���@�ƁA����Ɏ��Ԃ̎����������Ă��邩��ł��B
�@�@�@�y�P�V�z�R���f���T�ƒ�R�������ċN����s�v�c�Ȃ���
�𗬓d������P�j�g���̐����g���P�O�u�o�Ă����Ƃ��Ď������J�n���܂��B�܂��d���ɒ�R����Ȃ��A���̐�ɃR���f���T���Ȃ��Ō𗬓d���ɖ߂��Ƃ��܂��B
���̂悤�ȂȂ����͒�R�ƃR���f���T�̒����H�Ƃ����܂��B��R�̒l�����ۂɗǂ��g���P�����Ƃ��āA�R���f���T�̗e�ʃ��A�N�^���XX�b�������P�j���ɂ����
X�b���P�^�Q�����b���P�^�U,�Q�W�~�P�O�O�O�g���~�b���P�j���@
�@������b���v�Z����ƁA���ꂪ�P�O�O�����Ă��܂��܂��B���������ۂ̉�H�ł́A�قƂ�ǂ����̂悤�Ȑ��l�ɂȂ��Ă��܂��܂��̂ŁA
�@�ŏ�������R���f���T�̐Ód�e�ʂ́@�@�@�P�O�O�����̂P�t�@���b�h���P���e�i�}�C�N���t�@���b�h�j�@�@�@�@���g���܂��B
�b���P�^�U,�Q�W�~�P�O�O�O�g���~�P�O�O�O��
�@�@�@�@�@�@�@���i�O,�P�T�X�^�P�O�O�O�O�O�O�j�e���O,�P�T�X���e
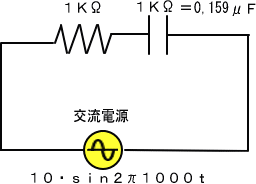
�P�j�g���ł͒�R�A�R���f���T�A�ǂ�����P�j���Ȃ̂Ō𗬓d���̓d���͂Q��������܂��B�܂������������ƂQ�j���ƂȂ�A�����d���F�h�́A
�h���P�O�u���Q�j�����O,�O�O�T�`�@�@�ł��B
���ۂ̓d�q��H�ł͂O,�O�O�P�`���P���`�i�~���A���y�A�j�̒P�ʂ��悭�g����̂Ł@�h���T���`�@�@�ƂȂ�܂��B
���ɒ�R�ƃR���f���T�̗��[�ɂ������Ă���d���̎����l�𑪂�ǂ��������
�d���h�~�q���T���`�~�P�j�����T�u�@�ɂȂ�܂��B
������𗬓d�����[�^�ő���A�����l�ɓ�����O,�V�{�̂R��T�u�������͂��ł����A�����l�͂ǂ�����T�u�߂�����܂��B
�T�u���s�[�N�l�Ɋ��Z����ƂP,�S�{�̂V�u�ɑ������܂����A�d���d�����s�[�N�l�P�O�u�̂��̂��Q����������A
�@�@�ǂ�����s�[�N�l�V�u�������Ƃ����̂́A��̂ǂ��������ł��傤�B
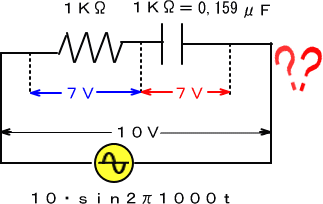
��R�͌𗬂ɑ��Ă������ɑ��Ă�����ɕς��͂���܂���̂ŁA����������̓R���f���T�ɗ����d���̈ʑ����ɂ��肻���ł��B
�܂�����܂ł̌o������A�R�C���ɂ��Ă��A���̐��i���������悤�Ȏ����N���肻���ł��B
�@�@�@�y�P�W�z��R�ƃR���f���T�̕��G�ȊW
�R���f���T�ƒ�R�̒���ƒ�R���m�̒���͂Ȃ�����قȂ�̂ł��傤���B
����͒�R��ƁA�R���f���T�ɂ͓d��������C�ȂǁA�S����������ł͂Ȃ��ł��傤���B
�P���g���łP�����̃R���f���T�ƂP�����̒�R��ɂ��āA�P�O�u�P���g���@�̐����g�d�����Ȃ��ƁA�ŏ��͂ǂ�����P�j���Ȃ̂Œ��ǂ������ÂT�u�œd���������܂��B
�@�@���ꂪ��R���m�Ȃ�A�����Ɣ����ÂŁA�߂ł����߂ł����Ƃ����Ƃ���ł��傤�B
�������R���f���T�̌𗬒�R�Ƃ́A�T�C���g�̂O�x����P�x�t�߁@�ł��̒�R�l�������Ă��邾���ŁA��{�I�ɂ͒~�d��ł��B
�����ŁA�����R���f���T�ɂȂ�������R��̐�ɂ����ƍ����d�����������Ȃ�A������R���f���T�������āA
�@�u�d�����ɂ͂����ƍ����d��������B���̐Ód�e�ʂ͂����Ə[�d�ł��邩��A������~�����I�v
�@�Ƃ킪�܂܂������Ă���킯�ł��B
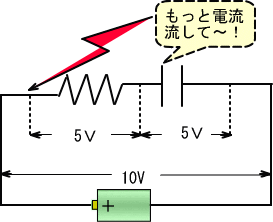
��R�͓d���̍����ق�����Ⴂ�ق��ɁA�f���ɓd���𗬂����i�Ȃ̂ŁA�R���f���T�̓d�����T�u���z���Ă��A
�@�����荂���d���d�����������A�d���𗬂������܂��B
�@�A���A�R���f���T�͂����̗~����ł͂Ȃ��A���d�̎��A�����Ƃ��̓d�����R�ɕԂ��̂ŁA��R�̓d�����V�u�Ə㏸���܂��B
�@�@�@�y�P�X�z��̓I�ȃR���f���T�ƒ�R�̊W
�ł͎��Ԃ�ǂ��ăR���f���T�ƒ�R�́A�d���Ɋւ�����Ƃ�ׂĂ݂܂��傤�B
�@�������A���܂�ׂ������Ԃ���ƁA�v�Z�����肪�����đ�ςł�����A�P�������@�R�O�����Ƃɕ����������g�Ɏ����@�K�i�g�@���g���܂��B
��̓I�ȊK�i�g�̍�����
�@�R�O���܂ł͂P�O�E�������R�O�����T�u
�@�U�O���܂ł͂P�O�E�������U�O�����W��U�U�u
�@�X�O���܂ł͂P�O�E�������X�O�����P�O��O�O�u
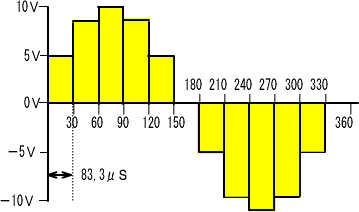
�@�Ƃ�����ł����A�P���Ȃ���P�Q�i�K�̌v�Z�́A���������ʓ|�ł��B
�܂��R�O���i�ނ̂ɕK�v�Ȏ��ԁ@���@��
�@�@�@�@�@�����P�b���R�U�O���P�O�O�O�~�R�O
�@�@�@�@�@���W�R��R���r�@�i���r���P�O�O�����̂P�b�j�ƂȂ�܂��B
�܂��P���g���łP�����̃R���f���T�b���O,�P�T�X���e�ƂP�����̒�R��ɂ�钼���H��p�ӂ��A�����ɊK�i�g�̓d���������܂��B
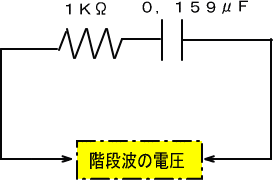
���̊ԁA�P�O�������R�O���ɂ�����T�u�����̉�H�ɂ����Ă݂܂��B�d�����㏸���n�߂����A�R���f���T�͂܂���ł��̂ŏ[�d�d������ʂɗ���܂��B
�Ƃ��낪��R�����邽�߁A�I�[���̖@���ɂ��d���h��
�@�@�@�@�@�h���T�u���P�������T���`�@�@�@����ȏ�͗���܂���B
�@�����łT���`���O��P�T�X���e�ɂW�R��R���r�����������Ƃ���ƃR���f���T�ɂ͉��{���g�̓d�������܂邩���A
�@�b�d���h���@��ό`�����@�d���h���^�b�@���g���Čv�Z���܂��B
�@���̂Ƃ��̃R���f���T�d�����d���P�Ƃ����
�@�d���P���T���`�~�W�R,�R���r���O��P�T�X���e���Q,�U�Q�u
���������ۃR���f���T�̗����d���́A�R���f���T�ɓd�C�����܂�ɂ�T���`��茸�����܂����A���d����Ƃ������������Ȃ̂ł���ŗǂ��Ƃ��܂��B
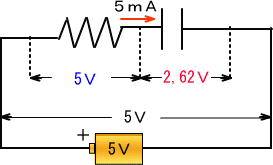
���̎��P�j���ɍő�T���`����Ă��܂������R�̗��[�ő�d���d���P���ƃR���f���T�̍ő�d�����@�h���P��
�d���P���h�q���T���`�~�P�j�����T�u
�h���P���T���`
 .
.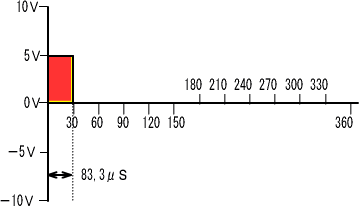
�@�Ƃ������ƂɂȂ�܂��B���̂悤�ɂ��ĂR�O�����ƂɂP�Q��ɂ킽���Čv�Z���A������O���t�ɂ��Ă݂�A���Ԃɋ߂Â������ł��B
�@�܂��K�i�g�͂P�i�P�i�̏オ����Ȃ̂ŁA���̓d����d�r�Ɍ����ĂĊG�ɂ��܂����B�����܂łő�P�i�K�͏I���ł��B
�@���ɂR�O������U�O���܂Ői�ނƓd���̊K�i�g�̓d���́@�W,�U�U�u�@�ł����A���̎����łɃR���f���T�̓d���́@�Q,�U�Q�u�@�Ȃ̂ŁA
�@�R���f���T�Ɠd���̓d������
�@�@�@�@�@�@�@�@�@�@�@�@�W,�U�U�|�Q,�U�Q���U,�O�S�u
�@�܂��d���ƃR���f���T�̊Ԃɂ͂P�����������Ă��܂�����A�R���f���T�ɗ����d���@�h���Q�@�́@�U,�O�S���`�@�ł��B
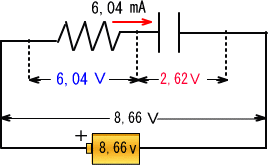
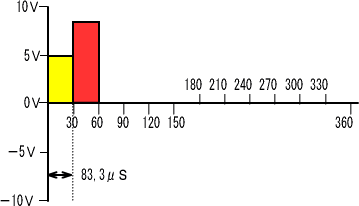
�@�����łR�O������U�O���܂ł̃R���f���T�d���̑������d��
�@�@�@�@�@�@�d���U,�O�S���`�~�W�R��R���r���O,�P�T�X���e���R,�P�U�u
�@���ꂪ�R�O���܂ł̃R���f���T�d���Q,�U�Q�u�ɉ����܂�����A�U�O���ł̃R���f���T�d�����d���Q�Ƃ����
�d���Q���Q,�U�Q�u�{�R,�P�U�u���T,�V�W�u�@
�d���Q���U,�O�S���`�~�P�������U��O�S�u�@
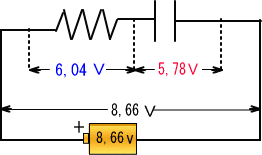
�@�����܂ł���Q�i�K�ł����A����ɂX�O���ł͓d�����ő�̂P�O�u�ɂȂ邽�߁A�R���f���T�Ɠd���̓d�����d���R��
�d���R���P�O�u�|�T,�V�W�u���S,�Q�Q�u�@�@
�@���ꂪ�P�����ɗ����̂Œ�R�ɗ����d���h���R��
�h���R���S��Q�Q���`
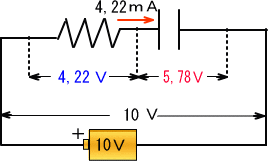
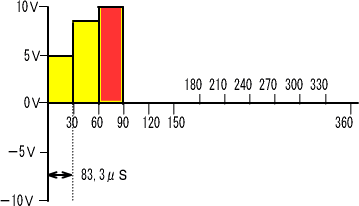
�@�����łU�O������X�O���̃R���f���T�̓d���������d���U�O���܂ł̓d���d���Q�ɉ������
�@�@�@�@�d���S,�Q�Q���`�~�W�R,�R���r���O,�P�T�X���e���Q,�Q�P�u
�@�@�@�@�d���R���T,�V�W�u�{�Q,�Q�P�u���V,�X�X�u
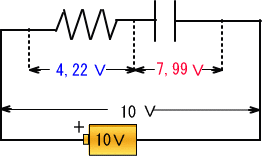
�@�Ƃ����d�����X�O���܂łɃR���f���T�ɏ[�d���ꂽ���ƂɂȂ�܂��B�����ő�R�i�K���I��܂�
�@�X�O������P�Q�O���ł͂W��U�U�u�ɓd���̓d����������n�߂܂����A�R���f���T�̓d���͂܂�������Ⴂ�̂ł���ɏ㏸���܂��B
�@���̓d���d���S��
�@�@�@�@�@�@�d���S���W��U�U�|�V��X�X���O��U�V�u�@�܂��d���́@�@�@�h���S���O��U�V���`
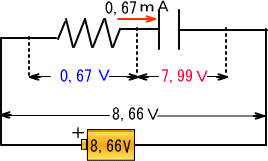
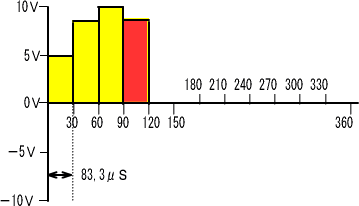
�@����ɂ��R���f���T�̑�������d����
�@�@�@�@�@�@�O�C�U�V���`�~�W�R��R���r���O��P�T�X���e���O��R�T�u
�@�����ŃR���f���T�̓d���d���S��
�@�@�@�@�@�@�@�@�d���S���V��X�X�{�O��R�T���W��R�S�u
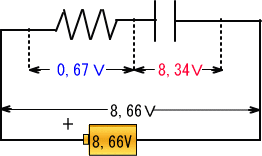
�@�P�Q�O������P�T�O���ł̓R���f���T�̓d�����d����荂���Ȃ邽�ߓd���̋t�����n�܂�A�d���ɂ̓}�C�i�X�̋L�������܂��B
�@�@�@�@�@�d���T���T�|�W��R�S���\�R��R�S�u�@�d�����@�\�R��R�S���`
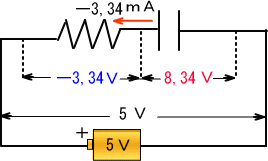
�@����ɂ��R���f���T�̓d���ቺ��
�@�@�@�@�@�\�R��R�S�~�W�R��R���O��P�T�X���\�P��V�T�u
�@�@�@�@�d���T���W��R�S�\�P��V�T���U��T�X�u
�ȉ��͏ȗ����܂���������\�ɂ܂Ƃ߁A�O���t�ɂ��Ă݂܂��B�A�� �d��(�u) �Ƃ����d���l�̓R���f���T�ɗ����d���l �h���i���`�j �ł�����܂��B
�܂������O���t�������Ⴒ���Ⴕ�܂����A�d���̓d���g�`�����킹�ĕ`�����݁A�ʑ�����������悤�ɂ��܂����B
�@�@�@�@�@�@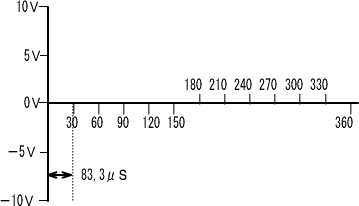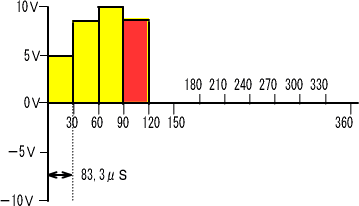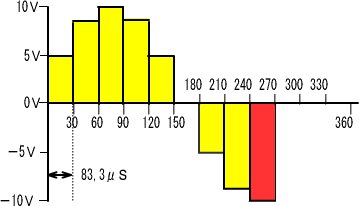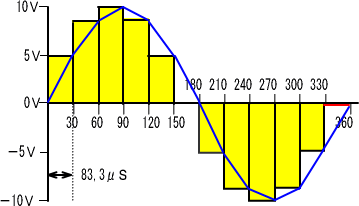
| �d���p�x | �O�� | �R�O�� | �U�O�� | �X�O�� | �P�Q�O�� | �P�T�O�� | �P�W�O�� |
| Er(�u)�@�@Ic�i���`�j | �O | �T,�O�O | �U,�O�S | �S,�Q�Q | �O,�U�V | �|�R,�S�O | �|�U,�T�X |
| Ec(�u) | �O | �Q,�U�Q | �T,�V�W | �V,�X�W | �W,�S�R | �U,�T�T | �R�A�O |
| �d���p�x | �Q�P�O�� | �Q�S�O�� | �Q�V�O�� | �R�O�O�� | �R�R�O�� | �R�U�O�� | �R�X�O�� |
| Er(�u)�@�@Ic�i���`�j | �|�W,�P�O | �|�V,�T�S | �|�S,�X�Q | �|�P,�O�P | �R,�P�W | �U,�T�P | �W,�P�O |
| Ec(�u) | �|�P,�P�Q | �|�T,�O�W | �|�V,�U�T | �|�W,�P�W | �|�U,�T�P | �|�R,�P�O | �P,�P�S |
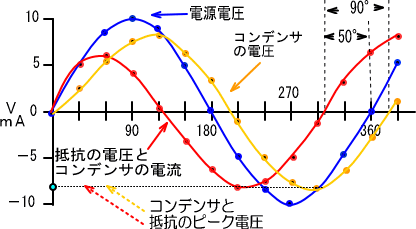
����͂R�O�����Ƃ̊K�i�g�ł��鎖�ƁA�d����������̃V���b�N��ԁi�ߓn���ۂƂ����j���v�Z�ɏo�Ă��邽�߁A
�@��R�ƃR���f���T�ɔ�������d���́@�P�Q�O����Q�P�O���ȂǂŁ@�W�u�@���x�ƍ��߂ɎZ�o����܂����B
�@���̂悤�ɓd���P�O�u�̐����g���R�ƃR���f���T�ŕ������Ă���̂ɁA�ǂ�����T�u�ȏ�ɂȂ鎖�����ĂƂ�܂��B
����ɃR���f���T�̓d���̈ʑ����A�R���f���T�̓d�����X�O���A�d���d�����T�O���߂��i��ł���l�q���킩��܂��B
����͌v�Z����������߁A���������鎮�̗ʂ����炷�K�v���������̂Ł@�R�O�����Ƃɒ��ׂ܂����B
�@�@���������ۂɁ@�P�O�����Ƃɒ��ׂĂ݂�ƁA�R�U�O�����߂��������肩��V�u�ɗ��������Ă䂭�̂��킩��܂��B
�@�@�����Ă��̎������d����
�V�u���P�j�����V���`�@�@�@�@�@�@�@�ƂȂ�
�܂����ꂾ���̓d�����A�P�O�u�̐����g�d���ɒ�R�ƃR���f���T�̍�����H���Ȃ����ۗ��ꂽ�̂ŁA���̌𗬂ɑ��鍇����R��
�P�O�u���V���`���P��S�j���@�@�ƂȂ�܂����B
�@���̍�����R���C���s�[�_���X�Ƃ�т܂����A�q��X�b���P�����P�����̎��A�������ꂽ�C���s�[�_���X�̒l���P,�S�����Ƃ������́A
�@�P�P�Œ��p�����ӎO�p�`�́A�Εӂ̒��������Q���P��S�P�ł��鎖���v���N�������܂��B
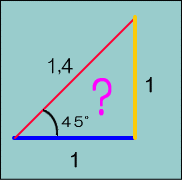
�܂��R���f���T�̓d�����@�T�O���d�����i��ł���_���A�Q���ӂR�p�`�̎Εӂ̊p�x���S�T���ł��鎖���v���N�������܂��B
�܂蒼�p�O�p�`�̒�ӂ��R�A���A�N�^���X�������Ƃ���A���̎��̃C���s�[�_���X�͎Εӂɓ�����A�d���̈ʑ��͎Εӂ̊p�x�ɂȂ�̂ł͂Ȃ����Ƃ������Ƃł��B
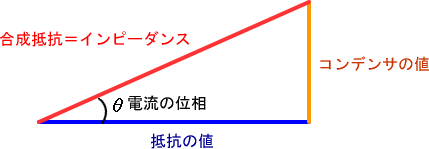
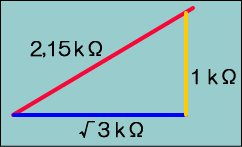
�����łP�����R�Œ��p�����O�p�`�̎Εӂ��Q�ł��鎖��O���ɁA�R���f���T�̃��A�N�^���X���P�j���A��R�����R�j���Ƃ��āA�R�O�������ɓ��l�̌v�Z�����Ă݂�A
�@�R���f���T�ƒ�R�łł���������R�͂Q�j���ɋ߂��l���o�邩������܂���B�v�Z�͏ȗ����܂��������͂Q��P�T�j���ł����B
�@�@�@�@�@�@�@�@�@�@�@
�@����ɒ��p���\������ӂ̔䗦���A�R�S�̒��p�O�p�`�̏ꍇ�A�Εӂ̒����͂T�Ȃ̂ŁA��R���R�j���A�R���f���T�̃��A�N�^���X�S�j���Ƃ��āA�R�O�������Ɍv�Z����ƁA�����͂T,�R�j���ł����B��͂�ǂ������̂�����ɓ���������ł������ł��B
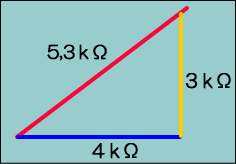
�R���f���T��R�C���ƒ�R�Ƃō\�����鍇���𗬒�R���C���s�[�_���X�́u�y�v�ŕ\���A�P�ʂ����ł�����R�q�ƃ��A�N�^���X�w�̑g�ݍ��킹�u�q�{X�v�ŕ\�L���܂��B
�y���q�{X
�@�@�@�y�Q�O�z�C���s�[�_���X�ƃs�^�S���X�̒藝
�܂���R�ƃR���f���T�̊W�������ׂĂ��܂��A����ł��������ꂽ�C���s�[�_���X�́A��ӂ��R�A���������A�N�^���X�Ƃ������p�O�p�`�̎Εӂ炵�����Ƃ��킩��܂����B
�@�@�������ꂪ��������A�ƂĂ����ɗ��̂��s�^�S���X�̒藝�ł��B
�s�^�S���X�̒藝�́A���p�O�p�`�̒��p���\�����Ă���Q�ӂ��A���ꂼ��Q�悵�Ă��瑫�����킹���������A�Εӂ̂Q�悾�ƌ������̂ł��B
�@��\�I�ȗ�͂R�ӂ��A�R�S�T�������̂ŁA�R�~�R�{�S�~�S���Q�T���T�~�T�@�@�ƂȂ�܂��B
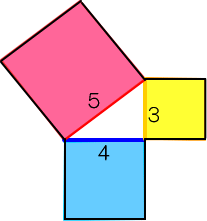
�܂��R�l�ƃ��A�N�^���X�l���킩���Ă���Ƃ��A
�@ ��ӂ��R�A���������A�N�^���X�Ƃ��ĎΕӂ̒������s�^�S���X�̒藝�Ōv�Z����A��R�ƃR���f���T�̍����C���s�[�_���X���킩��B
�A �Εӂ̒����ƍ����̔䗦�ɍ������������̒l���O�p���\�Ō�����A���̊p�x���d���Ɠd���̈ʑ����ɂȂ�B
�Ƃ������ƂɂȂ�܂��B�������R�O�������Œ��ׂ����A���܂�\�z�ƍ����Ă��Ȃ������A�R�S�T�̒��p�O�p�`�̏ꍇ���ɁA���x�͂P�O�������ɒ��ׂĂ݂܂��B
�@���A�N�^���X�͐�قǓ��l�A�P���g���̎��̐��l�ōl���܂��B
���̔䗦�Œ����R�̕ӂ��R���f���T�̃��A�N�^���X�P�����Ƃ���ƁA�����S�̕ӂ͒�R��Œ�R�l�͂S�^�R�����A�ƂȂ�܂��B
�܂��T�̕ӂ͍����C���s�[�_���X�T�^�R�������P,�U�U�V�����ł��B
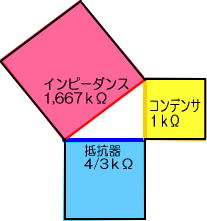
��������ɂP�O�u�P���g���̐����g�d�����Ȃ���Ɨ����d���@�h�ƃ��A�N�^���X�P�����̃R���f���T�ɔ�������d���d����
�h���P�O�u���P,�U�U�V�������U���`
�d�����P�����~�U���`���U�u�@
�Εӂ̌X�R�V���i�O�p���\���j
�ƂȂ�͂��ł��B
�����������҂����ɁA��قǍs�����v�Z���P�O�����ɕ������čs����
�d�����U�C�P�X�u
�Εӂ̌X�R�T��
�@�Ƃ��������킩��܂����B���̂悤�Ȏ������ʂ���A��قǂ�
�@
�ӂ��R�A���������A�N�^���X�Ƃ��ĎΕӂ̒������s�^�S���X�̒藝�Ōv�Z����A��R�ƃR���f���T�̍����C���s�[�_���X���킩��B
�A
�Εӂ̒����ƍ����̔䗦�ɍ������������̒l���O�p���\�Ō�����A���̊p�x���d���Ɠd���̈ʑ����ɂȂ�B
�@�Ƃ������̊m�M���[�܂�܂����B
�@�@�@�y�Q�P�z�R�C���ƒ�R
�R���f���T�ɂ��āA���낢�뒲�ׂĂ��܂������R�C���ł������悤�Ȏ����N����ł��傤���B
�܂��P���g���łw�k���P�j���̃��A�N�^���X�������R�C���̃C���_�N�^���X�k���v�Z���܂��B
�P�j�i���j���Q�����k���U,�Q�W�~�P�j�i�g���j�~�k�i�g�j
�k���P�j���P�j���U,�Q�W���O��P�T�X�g���P�T�X���g
�@�d���͑O�l�ω������܂��̂ŁA������C���s�[�_���X���P��U�U�V�����߂��ɂȂ�Η\���������������ɂȂ�܂��B
�@�����ňȑO�o�Ă����R�C���Ɠd�����Ƃ̊W���@�u�k�h���\�d���v�@�ɍēo�ꂵ�Ă��炢�܂��B
�@���̎���ό`�����
�h���\�d���^�k�@�@�@�ƂȂ�܂��B
�@���ꂾ���̏�����p�ӂ��Ď������n�߂܂��傤�B�ŏ��ɂT�u�d��������������Ƃ��A�R�C���͖�����̒�R�������܂��̂ŁA��R�ɗ����d���̓[���ƂȂ�A
�@�R�C���ɂ͂T�u�����̂܂܂�����܂��B�������₪�Ď����d��������܂�������܂ł̔����d���h��
�h���\�T�u�~�W�R�C�R���^�P�T�X�����\�Q�C�U�Q���`
�@����̓R�C�����������ꂽ�Ƃ��������R�̍ő�d����
�@�@�@�@�@�T�u���S�^�R�j�����R��V�T���`
�����ł��̎���R�ɗ����d����
�@�@�@�@�R��V�T���`�|�Q��U�Q���`���P��P�R���`
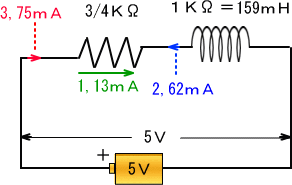
�@�Ƃ�����A���̓d�����S�^�R�j���ɗ����̂ŁA��R�̗��[�̓d����
�@�P��P�S���`�~�S�^�R�j�����P��T�Q�u�@
�@���̓d����d���̓d����������A
�@�T�|�P��T�Q���R��S�W�u�@�@
�@�@���ꂪ�R�O�x�ɂ����鎥���������̃R�C���̓d���ƂȂ�܂��B�ȉ��͏ȗ����܂������̂悤�Ȍv�Z�̌���
�y���P�O���U,�O�V�T���P,�U�S�U�j��
�ƂȂ��āA�P�C�U�U�V�����ɋ߂��l�ɂȂ�܂����B�R�C���ɂ��Ă��s�^�S���X�̒藝���ʗp�������ł��B
�@�@�@�y�Q�Q�z�R�C���ƃR���f���T�̓d���ŋN����l������
�`�j���U
�v�Z�ɂ���ĂR�X�O�����炢�܂łP�j�g���łP�j���̃��A�N�^���X�����A�R�C���ƃR���f���T�̓d���g�`����}���Ă݂�ƁA�d���O�̐��𒆐S�ɁA�㉺�őΏ̂ɂȂ��Ă��܂��B
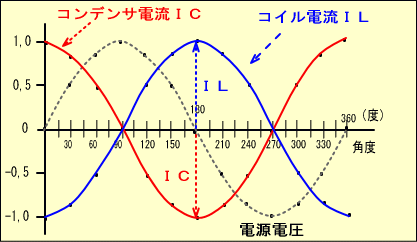
���̎�����A�����R���f���T�ƃR�C����ɂȂ��A���̗��[�ɂP�j�g���̌𗬓d���œd���𗬂����Ȃ�A�Е����v���X�̓d���������Ƃ��A�����Е����}�C�i�X�̓d�������āA
�@���������Z�����d���͂����O�u�Ƃ������ƂɂȂ�܂��B
�d���𗬂��Ă��d�����������Ȃ��̂́A���̎��g���̎�������R�l���قڂO���Ƃ������ƂŁA����U���ۂƂ����A�܂����̎��g�������U���g���Ƃ����܂��B
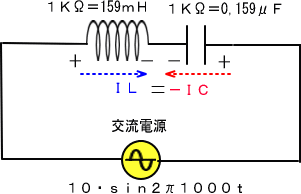 �@�@�@�@
�@�@�@�@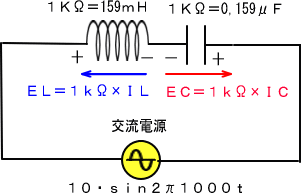
���������̎��A�d���O�u�Ƃ����̂͂����܂œd�����猩���O�u�ł����āA�R�C�����g�̓v���X�P�O�O�O�u�A�R���f���T���g�̓}�C�i�X�P�O�O�O�u�Ƃ�����������܂��B
�@����́u�ꌩ�ǍD�ȕ��͋C�ł��A�l�m�ꂸ�������Η����J��L�����Ă��闣�����O�̕v�w�B�v�Ƃ����̂Ɏ��Ă��܂��B
�ʂ̌���������ƁA�R�C���ƃR���f���T������ɂȂ��Ă����,���g������߂���ƁA�R���f���T�̃��A�N�^���X�w�b���傫���̂œd�������ꂸ�A
�@���g�����������Ă��R�C���̃��A�N�^���X�w�k���傫���A��͂�d��������܂���B
�@���U���g���͂��傤�ǂ��̒��ԓ_�ŁA�}�ɒ�R��������ꏊ�Ƃ����܂��B
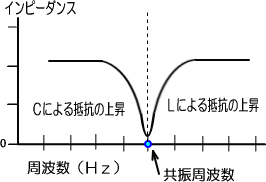
�a�j���U
����ɁA�R�C���ƃR���f���T�����ɂȂ��A���̗��[�ɓd���������Ă݂܂��B
����ƕЕ����v���X�����ɓd���𗬂����Ƃ���Ƃ��A�����Е����}�C�i�X�����ɓd���𗬂��܂��B
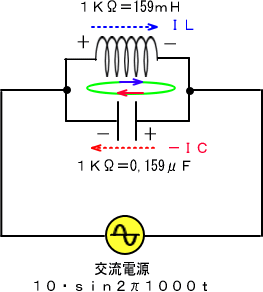
����͂��������A�R�C���ƃR���f���T��������Ȃ����ւ̒������œd���̂��������Ă���A�u�e���ȗ��l���m�̂������ɁA���҂������荞�����Ƃ���]�n�͂Ȃ��B�v
�@�ƌ����̂Ɏ��Ă��܂��B���̂��ߋ��U���g���Ɍ���A�d�������荞�߂܂���B
���̏�Ԃ���U���ۂƂ����A��R�l�͋��U���g���łقږ�����ɂȂ�܂��B
�ʂ̌���������Ύ��g�����Ⴗ����Ƃw�k�͂ǂ�ǂ�ቺ���ĉ�����R��������ԂɂȂ�A��������w�b���ቺ���āA��͂��R�������Ȃ�܂��B
���U���g���͂��̒��ԂŁA�}�ɒ�R�̑�����ꏊ�Ȃ̂ł��B
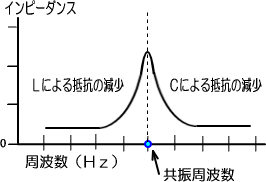
�@���U�͋��A�ŗL�U���A�ȂǂƂ������A�d�C�ɂƂǂ܂炸�A������_�I�ȕ����ɂ�������܂��B
�u�i�C�X�ȃ_�W�������������̂ɁA��������Ă���Ȃ������B�v�Ƃ����̂͂�������l�����̏��̋��U�_�ƃY���Ă��邩��ł��B
�@���U�̏����́@X�b��X�k�@�ł����A���̎��@X�b���P�^�Q���b�@X�k���Q���k�@�ł����玮������
�@�@�@�@�@�@�@�@�@�@�@�P�^�Q�����b���Q�����k�@�@�@
�@����������g�������o���悤�Ɏ���ό`�����
�@�@�@�@�@���~�����P�^�Q���~�Q���~�b�~�k
�@�@�@�@�@��²���P�^�S²���b�k
�@�@�@�@�@�����P�^�Q�����b�k�@
�@
�ƂȂ�A�Ō�̎��ɂb�Ƃk�̒l�Ă͂߂�ƁA���U���g�������v�Z�ł��܂��B�Ƃ��낪���ꂾ���ł͎��p�I�ł͂���܂���B
�d�C��H�͏���Ȃ�u�g���ĂȂ�ځv�ł���]�˂ł́u�g���Ȃ���Ȃ�˂��v�̂ł��B�����ŏo�Ă���̂��p�Ƃ����W���ł��B
�@�@�@�y�Q�R�z���U��H�ɂ����̂̂p
���U��H�́u�����v�́A����̎��g���ŁA�}�ɒ�R���傫���Ȃ����菬�����Ȃ����肷�鎖�𗘗p�����A�u�I���@�\�v�ɂ���܂��B
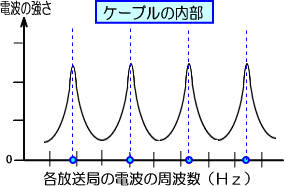
�e���r�̃`�����l�������������Ă��A�A���e�i��A���e�i����̃P�[�u������{�ł��ނ̂́A�P�[�u���ɓ����Ă����l�X�ȓd�g�̒�����A�ړI�̎��g���̓d�g���A�e���r���I�����Ă��邩��ł��B
 �@�@�@
�@�@�@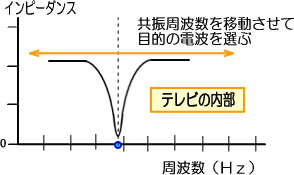
���̂悤�ȉ�H�ł́A�ǂ̒��x�̓d����d���ʼn�H�������Ă��邩���d�v�ɂȂ�܂��B
�e���r���d�g��I������`�����l����ւ��ŁA�Ⴆ�P�O�O�u�̓d���łP�O�����炢�̃��A�N�^���X�ɂ�鋤�U��H���������A���̑O��̓d���h��
�h���P�O�O�u���P�O�����P�O�`�@
���̎��̓d�͂o��
�o���P�O�O�u�~�P�O�`���P�O�O�O�v
�@�ƂȂ�܂��B
�@����ł̓`�����l����ւ������ŃI�[�u���g�[�X�^�[�P�䕪�ɂȂ��Ă��܂��A�d�C�オ�ܑ̖����Ȃǂƌ����ȑO�ɁA���M�ʼnЂ̊댯���炠��܂��B

�t�ɁA�T�O���ȉ��̒�R�ō\������Ă���d�C��H�łQ���{�A�܂�P�O�O�O�j���̃��A�N�^���X�ɂ����U��H�������Ă��āA�u���U���g���ł͒�R��������ɂȂ�܂��B�v
�@�ȂǂƂ����Ă��A�T�O������݂���P�O�O�O�j��������������܂�ς��܂���B
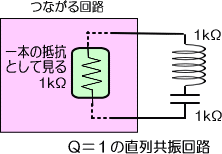
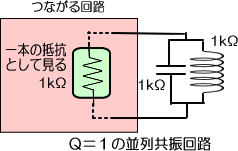
�����ŁA�܂��ɂȂ����H�́A���������̃C���s�[�_���X��P���Ȓ�R�Ƃ��Č��āA���̒�R�̒l���q�Ƃ���Ƃ�
�q���w�b���w�k
�@�ł���悤�ɋ��U��H�����A���̋��U��H�̂p�͂P���Ƃ����܂��B
 �@�@�@
�@�@�@
�`�j���U��H�̂p
���U��H�łp���P�̎��́A���U���g���łq�Ƃw�k��w�b�̑傫�����������̂ł����A�����q�̒l���P�O�{�ɂȂ�ƁA����Ɠ������A�N�^���X�������߂ɂ́A
�@�R�C�����R���f���T�����U���g���Ƃ͕ʂ̎��g���ł��̒l���������邵������܂���B
�Ⴆ�w�b���P�^�Q���b�@�łw�b���P�O�{�ɂ���ɂ͂b�ƂQ�͕ς��悤�������̂ŁA�����P�O���̂P�ɂ��܂��B
���l�ɂw�k���Q���k�@�łk�ƂQ�͕ς��悤�������̂ł����P�O�{�ɂ���Ηǂ����ɂȂ�܂��B
�@���̗l�q���O���t�ɂ���ƁA���ɊG�̂悤�ɂȂ�A���U��H�̒J�̕����A�L�����������Ӗ����܂��B
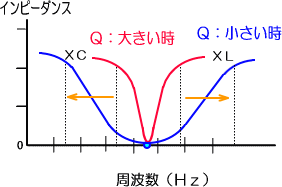
�@�p�͖{�����U�_�́A�R��J�̉s����\���Ă���̂ŁA���̏ꍇ�͂p�������������ƂɂȂ�܂��B
�@���U��H�ɂȂ����H�̃C���s�[�_���X���q���傫���Ȃ����Ƃ��A�p���������Ȃ����Ƃ������Ƃ́A�q�͂p�ɔ���Ⴗ��Ƃ������ƂŁA�q������ɓ����������o���܂��B
�@���U��H�̂p��
�@�@
�p���w�b�^�q���w�k�^�q�@�@
���̎��̈Ӗ��́A
�u���U��H�̂p���グ��ɂ́A���U��H���\������R�C����R���f���T�̃��A�N�^���X����H�̃C���s�[�_���X��荂���ݒ肷��B�v
�Ƃ������Ȃ�܂��B
�a�j���U��H�̂p
�@���U��H�ł�����R�q���P�O�{�ɂȂ�ƁA�w�b���P�O�{�ɂȂ���g���͂P�O���̂P�ɁA�܂��w�k���P�O�{�ɂȂ���g���͂P�O�{�̏ꏊ�Ɉڂ�܂��B
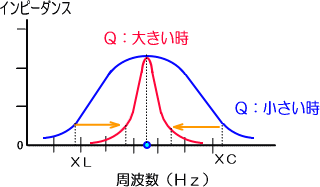
�@���U��H�ɂ����āA�C���s�[�_���X���㏸����R�̐��삪���܂�̂́A�p�������Ȃ鎖���Ӗ����܂��B
�@�q��
�p���q�^�w�b���q�^�w�k
�@���̎��̈Ӗ���
�@�u���U��H�̂p���グ��ɂ́A���U��H���\������R�C����R���f���T�̃��A�N�^���X���A��H�̃C���s�[�_���X���Ⴍ�ݒ肷��B�v
�@�p�͋��U��H�ɂƂ��āA�ǂ����ɗ��������߂��Ȑ��l�ł͂���܂����A�܂��̉�H�����\�ȕ��i�̐��l�ɍ��E����邽�߁A�قǂقǂɋ߂��l�őË�����̂����ʂł��B
�@���p�I�Ȃp�͂O��T���琔�S���炢�ɂȂ�܂��B
�܂��p�͎��R���ۂ�l�̐��_��Ԃɂ������āA�u���C�Ȃ��������ꌾ���l�����{�������B�v�ȂǂƂ����ꍇ�A���̌��t�����̐l�̓{��A����A�߂��݂̋��U�_�ł���A�p�̒l�����Ȃ荂�������@�����܂��B
���̐�͐��쒆�ł�
�@�@�@�y�Q�S�z�t�B���^�[
�t�B���^�[�Ƃ������t�ŁA�P�Ԑg�߂Ȃ̂̓^�o�R�̃j�R�`������������t�B���^�[�ł����A���̌��t�̒��ɂ́u�I�����ď�������v�Ƃ��u���肵�ď�������v�Ƃ����悤�ɁA
�@�@�Q�̓�����܂Ƃ߂��Ӗ����܂܂�Ă��܂��B
�I�[�f�B�I��H�̃t�B���^�[�͂قƂ�ǂ���R�ƃR���f���T�ō\������A�R���f���T�̃��A�N�^���X�̒l�ƒ�R�̒l���������Ȃ���g���ŁA
�@�d�����Q���������Ƃ����������g���܂��B���̎��́@���g�����J�b�g�I�t���g���Ƃ����A�t�B���^�[�̌��ʂ�����n�߂�|�C���g�������܂��B
���̏�Ԃ��A�J�b�g�I�t���g�������A��R���q�A�R���f���T�̗e�ʂ��b�A�R���f���T�̃��A�N�^���X���w�b���g�������ŕ\���ƁA�w�b�Ƃq���������Ƃ������Ƃ�
�w�b���P�^�Q���b���q�@
�@�ƂȂ�܂����A��������낢��ό`�����
�����P�^�Q���b�q
�b���P�^�Q�����q
�q���P�^�Q�����b�@�@�@�@�@�Ȃǂ��ł��܂��B
�t�B���^�[�̓I�[�f�B�I��H�̒��ŁA�𗬂̏����A�����̏����A������ቹ�̒����ȂǂɎg���܂��B
�`�j�𗬂̏����ƃn�C�J�b�g�t�B���^�[
�@����������R���f���T�ɂ���Ē����ɋ߂Â��Ă��𗬐����͎c���Ă��܂��܂��B�����ŃR���f���T�̐�ɒ�R���Ȃ��A
�@������x�R���f���T���A�[�X�ɗ��Ƃ��ď[�d�����鎖�ɂ���āA�X�ɒ����@�ɋ߂Â��܂��B
�@�����d���t�B���^�[�A�܂��̓��b�v���t�B���^�[�Ƃ����܂����A��R�����܂�傫���Ƒ�d�����A���̒�R��œd���ቺ���N����̂ŁA
�@�ő�d�����œd���d���̂P�O�p�[�Z���g�ቺ����Ɂ@���܂��B
�@�d���̓d���P�O�u�A�ő�d���P�O�O���`�Ƃ���ƁA��R�q�͂P�O���łP�u�̓d���ቺ���N����܂��B
�@�d�����g�������T�O�g���Ƃ���J�b�g�I�t����ȉ������ʓI�ɂȂ�܂��B
�@�R���f���T�̐Ód�e�ʂ��b�Ƃ���ƃ��A�N�^���X�w�b�̒l���P�O���̎��Ƃ�
�w�b���P�^�i�Q���~�T�O�~�b�j���P�O�i���j
�b���P�^�Q���q���P�^�i�Q���~�T�O�~�P�O�j
���P�^�P�O�O�O�����P�T�X�i���e�j
���̎����b�v���͔����ɂȂ�܂����A����Ɍ��ʂ��o���ɂ̓J�b�g�I�t���g�����P�O���̂P�̂T�g���ɐݒ肷��悭�A
�@���̂��߂ɂ̓R���f���T�̗e�ʂ��P�O�{�̂P�U�O�O���e�ɂ��܂��B
���̎��T�O�g���ɑ���R���f���T�̃��A�N�^���X�͂P���ŁA���b�v���͂P�O���̂P�ɂȂ�܂��B
����ɁA���̃��b�v���t�B���^�[�́A�R���f���T�b���P�T�X���e�̎��A�T�O�g���ȏ���J�b�g����n�C�J�b�g�t�B���^�[�Ƃ��l�����A
�@�P�O���̉�H�ɂȂ���Ƃp���P�ɂȂ�܂��B
�a�j�����̏����ƃ��[�J�b�g�t�B���^�[
����ǂ͋t�ɂǂ̒��x�̃��b�v��������̂����������o�������Ƃ���A�������ꂽ��̃R���f���T�ɂ����P�R���f���T�b���Ȃ��A
�@���̐�ɒ�R�q���Ȃ��ŃA�[�X�ɗ��Ƃ��܂��B
�@�R���f���T�͒����𗬂��Ȃ��̂Ō𗬂݂̂����o���܂����A��������[�J�b�g�t�B���^�[�ƍl���b�Ƃq�Ō������n�߂���̎��g������ݒ�ł��܂��B
���b�v���M���̌��o��ړI�Ƃ��邽�߁A���܂�d���̗ʂ�K�v�Ƃ��Ȃ��A�P�O�j�����x�̃C���s�[�_���X�̉�H�ɂȂ����邱�Ƃ�O��Ƃ��A�����T�O�g���Ƃ����
�b���P�^�Q�����q���P�^�i�P�O�O���~�P�O�j�j���O,�P�T�X�i���e�j
�b�j�ቹ�㏸�ƃ��[�p�X�t�B���^�[
���[�p�X�t�B���^�[�̓n�C�J�b�g�t�B���^�[�Ǝ��Ă��܂����A�J�b�g�I�t���g���ɂ�������̂��Q����܂��B
�@�ЂƂ̓n�C�J�b�g�t�B���^�[�̃J�b�g�I�t�Ɠ������������Ēቹ�̕����猩��Ƃ��̎��g����荂�����g���͒ቺ���A�u���[���I�t�v�Ƃ����܂��B
�@�����ЂƂ͂��̒ቺ���~�߂���g���ŁA�������g���̕����猩��ƁA�������Ⴂ���g������㏸���͂��܂�悤�Ɍ�����̂ŁA�u�^�[���I�[�o�[�v�Ƃ����܂��B
��H�̃C���s�[�_���X���P�O�j�Ƃ��Ăp���P�O�ɂ���ƍŏ��̃n�C�J�b�g�t�B���^�[�̒�R�q�P�͂P�O�O�j���ŁA���[���I�t���Q�O�g���Ƃ���ƁA�K�v�Ȃb��
�b���P�^�Q���E�Q�O�E�P�O�O�j���O,�O�S���e
���̂܂܂ł͂Q�O�g���ȏ�̎��g���œd���͂ǂ�ǂ�ቺ���܂����A������~�߂���g���^�[���I�[�o�[���P�O�O�g���Ƃ���ƁA
�@�R���f���T�ƃA�[�X�̂������ɒ�R�q�Q������܂��B���̂Ƃ��q�Q���P�O�O�g���łw�b�Ɠ����ɂȂ����ȏ㍂�����g���œd�����ቺ���܂���B
�P�O�O�g���ł̂w�b���g���ɔ���Ⴕ�A�Q�O�g���̎��̂T���̂P�ƂȂ�܂��B�P�O�O�j���̂T���̂P�͂Q�O�j���ł��̂ŁA�q�Q�������Q�O�j���ɂ���Ηǂ����ɂȂ�܂��B
�c�j�����㏸�ƃn�C�p�X�t�B���^�[
�n�C�p�X�t�B���^�[�̓��[�J�b�g�t�B���^�[�́u���[���I�t�v�ƁA�d���̒ቺ���~�߂�u�^�[���I�[�o�[�v�̒�R���琬��܂��B
��H�̃C���s�[�_���X���P�O�j���Ƃ��Ăp���P�O�Ƃ���ƁA���[�J�b�g�t�B���^�[�̃��[���I�t���g�����P�O�j�g���łP�O�O�����̃��A�N�^���X�����R���f���T�̂b��
�w�b���P�^���Q�E�P�O�j�E�P�O�O�j���O,�O�O�O�P�T�X���e
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���P�T�X���e�i�s�R�t�@���b�h�j
�s�R�̓}�C�N���̂���ɂP�O�O�����̂P�ŁA�P�����̂P��\���܂��B���̌�ɂP�O�O�j���̒�R�ŃA�[�X�ɗ��Ƃ��ƁA���[�J�b�g�t�B���^�[���o���܂����A
�@���̂܂܂ł͂P�O�j�g���ȉ��̎��g���łǂ�ǂ�d�����ቺ���܂��̂ł�����~�߂���g�����S�j�g���Ƃ��܂��B
�S�j�g���ɂ�����P�T�X���e�̃��A�N�^���X�͂Q��T�{�̂Q�T�O�j���ł��̂ŁA�Q�T�O�j���̒�R���P�T�X���e�ɕ���ɂȂ���ƁA
�@����ȉ��̎��g���œd���̒ቺ���N���܂���B
�y�Q�V�z�g�����X�ƃR�C��
�g�����X�́A�^��ǃA���v�ɂƂ��čŏd�v���i�ł��B�g�����X�ƃR�C���͌��t�̎g�������������ŁA�ʏ�͂ЂƂ̓S�c�i�R�A�j�ɕ����̃R�C���������Ă�����̂��g�����X�ƌ����ꍇ�������A�e�R�C���̓��͑����P�����A�o�͑����Q�����ƌĂт܂��B�g�����X�̂P�Ԗڂ̖����̓C���s�[�_���X�̕ϊ��ɂ���A�d���̕ϊ�������Ɋ܂܂�܂��B�����P�̖����̓A�C�\���[�g�i�����A�≏�j�ŁA�ʑ��̔��]������Ɋ܂܂�܂��B
�`�j�C���s�[�_���X�Ɠd���ϊ�
�g�����X�̂P�����ƂQ�����̓d����̓R�C���̊�������ƈ�v���܂��B�Ⴆ�P�����P�O�O��ŁA�Q�����Q�O�O���Ă���g�����X�̂P�����ɂP�O�u������A�Q�����ɂ͂Q�O�u������܂��B���@�����g�����X�̒��ł͓d�C�A���C�A�d�C�ƕϊ������̂ŁA���z��Ԃł͓d�͂̑����͂���܂��A���ۂ̓R�A����������鎞�A�R�A�ނ̎��N�Z�ƁA�����̒�����R�A�����ǂ����ɂ��Ód�e�ʂő������N���܂��B
�����ŗ��z��Ԃ̃g�����X���������Ƃ��āA�P�����P�O�u�������P�`�d���������P�����̓d�͂o��
�o���P�O�u�~�P�`���P�O�v�@�@�ł��B
�Q�����͂Q�O�u�Ȃ̂ŁA�P�O�v�̓d�͂����̂܂܂Q�����ɓ`���Ƃ���A�����d���h�́A
�h���P�O�v���Q�O�u���O,�T�`�@�ƂP�����̔����̓d���ɂȂ�܂��B
���̎��P�����̃��A�N�^���X�w�k�P��
�w�k�P���P�O�u���P�`���P�O��
�@
����Q�����̃��A�N�^���X�w�k�Q��
�w�k�Q���Q�O�u���O,�T�`���S�O��
���̂悤�Ɋ����䂪�Q�{�ɂȂ�ƃ��A�N�^���X��͂S�{�ɂȂ�܂��B��ʓI�ɂ͊�����̓�悪���A�N�^���X��ƂȂ�܂��B�Ƃ���ŃR�C���̃��A�N�^���X�w�k���Z�o����ɂ́@�w�k���Q���k�@�ł��B���̎��̉E�ӂƍ��ӂ̊W����A���A�N�^���X�w�k���S�{�ɂȂ鎞�A�u�k�v���Ȃ킿�R�C���̃C���_�N�^���X���S�{�ɂȂ鎖���킩��܂��B
�܂�R�C���̊������Q�{�ɂ���ƁA�C���_�N�^���X�͂S�{�ɂȂ�܂��B
�a�j�A�C�\���[�g�ƕ����ƈʑ����]
�g�����X�͓d�C���P�C�ɕϊ����āA�ԐړI�ɓd�C��������̂ŁA�R�C���ǂ����͓d�C�I�Ɍ𗬁A�����A�ǂ���ɑ��Ă��S���≏����Ă��܂��B���ꂪ�A�C�\���[�g�ł��B�܂��d�����ϓ����Ȃ��ƂQ�����ɓd�����������Ȃ��̂ŁA�������܂𗬂���𗬕������������邱�Ƃ��o���܂��B
����ɒʏ�g�����X�̃R�C���͊����n�߂���E���ɂP��������������A�Q���������������Ŋ����܂��B���̏�Ԃŗ������A�d���̊����n�߂Ƀ}�[�N��t���A�}�[�N�̕t�����P�����ƂQ�����̐��ǂ������A�[�X�Ƃ���A�����̊����I���œd���̈ʑ��������ɂȂ�܂��B
�ʑ��������Ƃ́A�P�����������g�̃v���X���ɂȂ��Ă��鎞�A�Q�����������v���X���ɂȂ��Ă���Ƃ������ł��B������t�ɗ��p���āA�Q�����̊����I����A�[�X�ɗ��Ƃ��A�t���̌𗬓d�����Q�����̊����n�߂�����o���܂��B���ꂪ�ʑ����]�ł��B
�y�Q�W�z�g�����X�̈ʑ��̉�]�i�ω��j
�g�����X�͏d���̑�p��I�u�W�F�ɗ��p�����ꍇ�������A���ꂪ�P�̂Ŏg���鎖�͖����A�K�����̃C���s�[�_���X����������H���ڑ�����܂��B�܂��g�����X�̓R�C�����琬�藧���Ă��܂��B�ȏ�̂Q�_����A�g�����X�̎g�p�ɂ͐ڑ��C���s�[�_���X���R�ƌ����Ă��A�R�C���ƒ�R�̒����H�ƌ��Ȃ������L�����Ɨ\���ł��܂��B
��R�ƃR�C���̒����H�ł͒�R�̑傫���p�O�p�`�̒�ӁA�R�C���̃��A�N�^���X�p�O�p�`�̍����Ƃ��č��Εӂ������C���s�[�_���X�ł��B���̎��A�d���̒x��͒�ӂƎΕӂŏo�����p�x���ŕ\���܂����A���g�����ω��������A���̊p�x���ǂ��ω����邩�l���Ă݂܂��傤�B
�P�T�X���g�̃C���_�N�^���X������R�C���́A�P�j�g���łP�j���̃��A�N�^���X�������܂��B���̃R�C���ƂP�j���̒�R�ɂ�钼���H�̏ꍇ��R�ƃ��A�N�^���X�ō���钼�p�O�p�`�́A�P�P�̓ӎO�p�`�Ȃ̂ŎΕӂ̊p�x�ƒ����͂S�T���Ɩ�P��S�ɂȂ�܂����A�C���s�[�_���X�Ō����u�P��S�j���œd���̒x���p�x�S�T���v�ƂȂ�܂��B
����𗪂��ď������ɂ�
�y���P,�S�j���S�T���@�u�P,�S�L���A�p�i�����j�S�T�x�B�v
�܂��́@�y���P,�S�j���i�^�S�j�u�P,�S�L���A�p�i�����j�S���̃p�C�B�v
�ȂǂƏ����܂��B
�����Ŏ��g�������Q�{�̂Q���ɂȂ����Ƃ���ƁA�R�C���̃��A�N�^���X�́u�Q�����k�v����u�Q���Q���k�v�@�܂胊�A�N�^���X���Q�{�ɂȂ�܂��B���A�N�^���X�͍����Ȃ̂ŁA�������Q�{�ɂȂ������̎Εӂ��v�Z���܂����A�����Ńs�^�S���X�搶�ɓo�ꂵ�Ă��������܂��B�Εӂ̌v�Z�������
���i�P�~�P�{�Q�~�Q�j�����T���Q,�Q�S�j��
�p�x���͂܂��킩��܂��A�����Q�A�ΕӂQ��Q�S�ƂQ�ӂ̒������킩�����̂Ł@�@�@
�r���������������ΕӁ��Q���Q,�Q�S���O�A�W�X
�Ƃ������͂��Ă��܂��B�����ŁA���̎������̒l���A�O�p���\���g���ċ��߂Ă݂܂��傤�B
�O�p���\�łr���������O,�W�X�̎��A�����ǂ̒l���������O�x���珇�ɒ��ׂĂ䂭�ƁA�r�����U�R���̎��ɒl���O��W�X�P�O�Ə����Ă���A���ꂪ�P�ԋ߂��l���ƍl�����܂��B����ɂ�������U�R���Ƌߎ��l���o�����Ƃ��o���܂����B
�ȏ�̂��Ƃ���P�j���ƂP�T�X���g�ɂ�钼���H�̂Q�j�g���ł̃C���s�[�_���X�y��
�y���Q��Q�S�j���U�R��
���l�ɑ��̎��g���ł����ׂ��
�P�O�O�g���ł́@�@�@�y���P�O�O���U��
�T�O�O�g���ł́@�@�@�y���P,�P�Q�j���Q�S��T��
�P�O�j�g���ł́@�@�@�y���X,�X�U�j���W�T��
�@�@�P�O�O�j�g���ł́@�@�y���X�X,�X�j���W�X��
���̂悤�ɂP�j�g���ŃR�C���̃��A�N�^���X�����߂�ƃI�[�f�B�I�ш悾���ł���O������X�O���Ƃ����傫�Ȉʑ��p�̉�]�ƂP�O�O�{�ȏ�̃C���s�[�_���X�̕ω����N���܂��B
�y�Q�X�z�g�����X�̈ʑ��̈��艻
�ʑ������艻����ɂ́A�P�O�j�g���ƂP�O�O�j�g���ł��܂荷���o�Ȃ������A�q���g�ɂȂ肻���ł��B�����ōŏ������̎��g�����P�O�O���̂P�ɂ��āA�P�O�g���ōl���Ă݂܂��ƁA�P�O�g���łP�j���̃��A�N�^���X�����ɂ́A�P�O�O�{�̃C���_�N�^���X������Ηǂ����ɂȂ�܂��B
�P�T�X���g�̂P�O�O�{�͂P�T��X�g�ɂȂ�܂����A���̃R�C���̂Q�O�g����P�O�O�g���̃C���s�[�_���X�͑O�̏͂̂Q�j�g����P�O�j�g���̌v�Z�����̂܂ܓ��Ă͂܂�܂��B�����ł��낢��Ȏ��g���Ōv�Z�����
�y�i�Q�O�g���j�@�@���Q,�Q�S�j���U�R��
�y�i�P�O�O�g���j�@���X,�X�U�j���W�T��
�y�i�P�j�g���j�@�@���X�X,�X�j���W�X��
�y�i�P�O�j�g���j�@���X�X�X,�X�j���W�X��
�y�i�P�O�O�j�g���j���X�X�X�X,�X�j���W�X��
���̂悤�Ɋ���g���������鎖�ɂ���ĂP�j�g���ȏ�͂قƂ�Ljʑ����ω������A�P�O�O�g���ɂ����ĂP�S���A�Q�O�g���ł͂R�U�����x�̕ϓ��ł��݂܂����B
�������Ĉʑ��ɂ��ẮA�Ȃ�Ƃ����肳�������̂́A�C���s�[�_���X�͑��ς�炸�ǂ�ǂ�㏸���Ă��܂��B�C���s�[�_���X���㏸����Ɠ����d���������Ă��d��������Ȃ��̂ŁA���g���������قǃR�A���������ɂ����Ȃ�͂��ł��B����ł͍������g���قǃg�����X�̂P��������Q�����ւ̓d�͓]�����\���ቺ���鎖�ɂȂ��Ă��܂��܂��B�g�����X�̓]�����\�����g���ɂ���Ăǂ̂悤�ȓ`�B�����������̂��Ȗ��ɒ��ׂ��O���t���A�g�����X�̎��g�������Ƃ����܂��B
�y�R�O�z�g�����X�̃C���s�[�_���X�̈���
�C���s�[�_���X�̏㏸�́A�U�����A�N�^���X�����g���ɔ�Ⴕ�ď㏸���邩��ł����A�g�����X�͂����̃R�C���ł͂Ȃ��A�Q�����̃R�C��������܂��B�����łP�����ƂQ�����ɓ������������R�C���������āA�Q�����̃R�C���ɂP�O�j���̒�R���Ȃ��܂��B
�𗬓d������P�����ɂP�O�u�A�P�j�g���̌𗬓d����������ƁA�P���ƂQ���̊����䂪�P�P�ł�����A�Q�����ɂ��P�O�u�A�P�j�g��������܂��B����ĂP�O�j���̒�R�ɂ͂P���`�̓d��������鎖�ɂȂ�܂��B���Ȃ݂ɂQ�����ɂȂ����R�ג�R�Ƃ������܂��B
�����Ŏ��g�����P�O�j�g���ɂȂ��Ă��d���͊����̔䗦�ł��܂�̂ŁA��͂�Q�����ɂ͂P�O�u���������A�P�O�j���̒�R�ɂP���`�̓d��������܂��B�Ȃ��R�C���̃��A�N�^���X���㏸���Ă��d�͂̓`�B�����Ȃ��Ȃ��̂ł��傤���B�܂��͉����𗧂Ă܂��B
���g���������Ȃ��ă��A�N�^���X���㏸���A�d��������ɂ����Ȃ�̂́A���ꂾ����ʂ̎������R�A�ɑ��s�����Ƃ��邩�炾�Ƃ���A�����ɂ���͑�ʂ̔��d�\�͂��R�A���甭�������ƌ����Ӗ��ł͂Ȃ��ł��傤���B
�ʂ̕\��������A�P�����Œ�R�𑝂₻���Ƃ��Ă��Q�����������ǂ����͂�d�͂ɕϊ����Ă��܂��̂ŁA�S�c�́u���̓C�����I�v�Ƃ�����R�����܂葝���Ȃ��A�������A�N�^���X�̏㏸�������ł���̂ł͂Ȃ��ł��傤���B�����ňȑO�o�Ă���
�k�h���v�����d��
�Ƃ������̈Ӗ���������x�l���Ă݂�ƁA
�u�k�w�����[�ɂh�A���y�A�d�������ꂽ���ɍ��ꂽ����
�d�{���g�̓d�������b�Ԕ��d�ł���B�v
�ƍl���Ă��܂����B�����Ă��̎��̂��Ƃ́u�P�^�Q�����v�ł����B
�����ŁA�Ȃ����̂悤�ȋL���̓��������������ԂȂ̂����A�����炢�̈Ӗ����܂߂Đ������܂��B���g�����Ƃ������̂͂P�b�Ԃɉ���U�����Ă��邩��\���L���ł����āA
�����U���^�P�b���U�������P�b�@�@
�Ə����܂��B���̂��Ƃ����L���̐����������Ă͂߂Ă䂭�ƁA
�����P�^�Q�����P�^�i�Q���~�U�������P�b�j
���P�b�^�i�Q���~�U���j
�܂�P�b�Ԃ��Q���ƐU���Ŋ������u���ԁv�����Ȃ̂ł��B
�Ⴆ�P�O�g���ł͂����P�O��^�b�ł�����A������قǂ̎��ɂ��Ă͂߂�
�����P�^�Q�~�P�O�^�b���P�^�U�Q,�W���O,�O�P�T�X�b
�����ł��Ƃ̎��ɖ߂�ƁA
�k�h���v�����d���@�Ɂ@�����P�^�Q�������Ă͂߂��
�v�����d�^�Q��
�ƂȂ�܂��B����œd���Ɠd���Ǝ��g���̊W���v�Z�ł������ł��B
���̎���ό`�����
�d���Q���v��
���̎��̈Ӗ����l���Ă݂�ƁA���̋����v�������Ȃ�A�Ⴆ�Ύ��g�������Q�{�ɂȂ�Ɠd���d���Q�{�ɂȂ�܂��B�܂肆�������Ȃ�قǔ��d�����d���d���傫���Ȃ�ƌ����܂��B
���ɓd���d�����ɕۂ��A���g�������Q�{�ɂȂ�Ƃv���͔����ɂȂ�܂��B����͎��g�����������Ȃ�قǁA���̎��͂v�����キ�Ă��d���ɕω��������ƌ������ł��B
���������͂̋����͓d�͂��R�C���ɂ���ĕϊ����ꂽ���̂Ȃ̂ŁA���͂��キ�Ȃ����̂ł́A���g���̏㏸�Ƌ��ɁA�g�����X�̓`�B�������ቺ����͂��ł��B����ɂ�������炸�A���ۂɂ͒ቺ���N����܂���B����̓R�A�ȊO�̉������R�A�̑�������āA�Q�����̃R�C���Ɏ��͂�`�B���Ă��邩��ł͂Ȃ��ł��傤���B
���̓R�A���̂��̂̎����ɂ��d�͂̓`�B�͒ቺ���Ă���̂ł����A�R�A��������̋�Ԃ���������āA���͂ɂ��d�͂̓`�B����`���͂��߂�̂ł��B�������Ė{�����̃C���_�N�^���X���������g�����X�ɂ́A���̎���ɂ����ƃC���_�N�^���X�̒Ⴂ�A�g�����X�Ƃ��Ă̓`�B�H��������ł��������āA�d�͂��P���R�C������Q���R�C���ւƓ`�B�o����̂ł��B�������Ⴂ�̂͂����܂œ`�B�H�̃C���_�N�^���X�ł����āA�g�����X�̃R�C�����̂��̂̃C���_�N�^���X���ቺ���Ă���̂ł͂���܂���B
���̂悤�Ȏ��͂P���R�C�������̂Ƃ��ɂ͉��̈Ӗ��������������ŁA�Q���R�C���������āA��������d�͂����o�����Ƃ������A���߂č�p���錻�ۂł��B
����ɁA���g���������Ȃ�قǃR�A�̐ӔC���y���Ȃ�Ƃ��������A���̌��ۂ͈Ӗ����܂��B���g���������Ȃ�قǎ��͂��������₷���Ƃ������́A�R�C���̊����������炵����A�R�A�������������肵�Ă��ǂ��Ƃ������ƂɂȂ�A�g�����X���̂��̂����^�ɍ��鎖���Ӗ����܂��B
���ہA����Ɏ��g���������Ȃ����d�g�����������g��H�ł́A���͂�R�A���s�v�ɂȂ邱�Ƃ������Ȃ�܂��B�R�A�������R�C���ł͉�����������邩�ƌ����ƁA��Ԃ���������A��Ԃ����ɖ߂낤�Ƃ���͂��A���͂�d�͂ɖ߂��܂��B��������ԂƂ͋�C�̎��ł͂Ȃ��A�n������܂߂��F����Ԃł��B����Ɏ��g���������Ȃ�ƁA�R�C�����u�����v�ƌ��������s�v�ƂȂ��ĂT�Z���`�ʂ̂����̓d���ł��R�C���̖������͂����܂��B�ł����璷���z���͍����g�ł͌�@�x�ł��B
�F����Ԃ̎����ň�Ԑg�߂Ȃ͉̂q�������ł��傤�B���������F����Ԃ�d�g������`���̂́A���������͂��̏ꏊ���A�Ȃ����ω����Ă��邩��Ȃ̂ł��B
�y�R�P�z�g�����X�̎��g�������̕ω�
�`�j���̒ቺ
�@�P�T��X�g�̃C���_�N�^���X���P�O�g���łP�j���̃��A�N�^���X�l���������A�d�����̃C���s�[�_���X���P�O�j���Ȃ�A�P�j���ǂ����œd���͂Q��������Ă��܂��܂��B�Q�����ƌ����Ă��d����
�P�O�����Q���V,�O�V�u
����܂����A�P�P�̊����̃g�����X�ł́A�Q�����������d�����o�Ă��܂��B�����d�͂ōl���Ă݂܂��傤�B
�@�d�����P�O�u�̎����ג�R���P�O�j���Ȃ�Η����d�����P���`�ł��邱�Ƃ���A�d�͂o�́A
�o���P�O�u�~�P���`���P�O���v
�V,�O�V�u�̎��͓d�����V,�O�V���`�ɂȂ�̂�
�V,�O�V�u�~�V,�O�V���`���T��O�O���v
���̎��̂P�j���̒�R�͂P�����ɂȂ����H�̃C���s�[�_���X�̑���ł��B�����Ńg�����X�̃��A�N�^���X���P�����ɂȂ����H�̃C���s�[�_���X�Ɠ����ɂȂ鎞�A�`�B�ł���d�͂������ɂȂ��Ă��܂������킩��܂��B��H�̃C���s�[�_���X������ɍ����Ȃ������́A�����ƍ������g��������̒ቺ���n�܂�܂��B
�@���Ƃ��Γ�����R���P�O�j���̎��́A�C���_�N�^���X�P�T,�X�g�̃R�C���̃��A�N�^���X���P�O�j���ɂȂ�P�O�O�g������A�d�����ቺ���鎖�ɂȂ�܂��B
�@�d�����̃C���s�[�_���X��d���̓�����R�Ƃ����܂����A������R�������Ȃ��Ă��������o���Ȃ��悤�A�[���ȃ��A�N�^���X�������߂ɂ́A�傫�ȃC���_�N�^���X���K�v�ɂȂ�܂����A����ɂ͊����𑝂₷�K�v������܂��B�����𑝂₷�����ł̓R�C���̒�����R�������Ă��܂��̂ő����d�����g���K�v������A�g�����X�͂܂��܂��傫���d���Ȃ�܂��B
�a�j����̒ቺ
���z��Ԃ̃g�����X�ł͎��g�����㏸���Ă��P�����ƂQ�����̓d����͊��������Ō��܂�܂����A���ۂ̃g�����X�ł́A�R�C���̊�����������ƁA�C���_�N�^���X�������锼�ʁA���_���o�Ă��܂��B�܂��d���̒�����������̂Œ�����R���ӂ��܂��B�d���͓��𒆐S�ɍ���Ă��܂����A�d�C��R���S�������ƌ����킯�ł͂Ȃ��A�͂��Ȃ����R�������܂��B
���ꂪ���S���[�g���ɂ��Ȃ�ƁA�d�C��R���ӂ��܂��B�����œd�����������ꂽ�Ƃ��A�R�A�̎����ƊW�����d�����������āA�g�����X�̓`�B�ɑ������N���܂��B
�܂������͓d���ǂ����������߂Â�����ԂȂ̂ŁA�͂��Ȃ�����R���f���T���\�����܂��B���ꂪ��ʂ̊����ł͑傫�ȐÓd�e�ʂƂȂ��ăR�C���ɕ���̃R���f���T���Ȃ�����ԂɂȂ�܂��B���̃R���f���T�������ԗe�ʂƌ����A�d���̓�����R�Ƒg�ݍ��킳��ăn�C�J�b�g�t�B���^�[�����܂��B
�Ⴆ�Ί����ԗe�ʂ��T�O�O���e�A�d���̓�����R���P�O�j���Ƃ���ƁA����ɂ����ꂽ�n�C�J�b�g�t�B���^�[�̃J�b�g�I�t���g������
�����P�^�Q���b�q���P���U,�Q�W���T�O�O���e���P�O����
���R�P,�W�j�g���@�@�@�@�ƂȂ�܂��B
���̐��l�̓I�[�f�B�I��H�Ƃ��Ĕ����ȂƂ���ł��B�����P�̗v���̓R�A�̍ގ��ɂ���܂��B�R�A�͓d��������Ď����o����܂ŁA�ޗ��ɂ���Ĕ����̃X�s�[�h���قȂ�܂��B�����̒x���ޗ��ł̓��O���������������Ȃ������̂悤�ɁA�����ɒ����čs�����A�ڂ��茩�Ă��邾���Ƃ�����ԂɂȂ�܂�����A���܂������`�B���鎖���ł��܂���B
�y�R�Q�z�g�����X�̋��U�Ƃp
�܂������ԗe�ʂƃC���_�N�^���X�����U��H���\�����܂����A���̎��g���F���͂w�k�Ƃw�b���������Ȃ�Ƃ��ŁA
�����P�^�Q���k�b���P���U,�Q�W�����i�P�T,�X�g�~�P�O�O���e�j
�@�@���R�X�X�O�g��
�@���̎��g���ŃC���s�[�_���X���ɂ߂č����Ȃ�͂��ł����A���ۂɂ͂p�̑傫�����m�F����K�v������܂��B�R�C���̃��A�N�^���X�w�k�Ɗ����ԗe�ʂw�b���v�Z�����
�w�k���Q�����k���U,�Q�W�~�R�X�X�O�~�P�T,�X
���S�O�O�j���i���w�b�j
�d���̓�����R���P�O�j���Ƃ���ƕ��U��H�̂p��
�p���q�^�w�k���P�O�^�S�O�O���O,�O�Q�T
���̂p�͎��g�������ɂǂ̂悤�ȉe��������̂ł��傤���B���S���g�����R�X�X�O�g�y���S�j�g���ł�����A���̃C���s�[�_���X�㏸�n�_�����P�Ƃ����
���P���S�j�g���~�O,�O�Q�T���P�O�O�g��
����̃C���s�[�_���X�㏸�n�_�����Q�Ƃ����
�@�@�@�@�@���Q���S�j�g�����O,�O�Q�T���P�U�O�j�g��
�ƂȂ��č���ł͂قƂ�ǎ��g�������ɉe�������������킩��܂����B���������ł͎��肪�L�肻���ł��B
�y�R�R�z�Q���R�C���̉e��
�g�����X�̂P���R�C���ɓd�������ꂽ���A�Q���R�C���ɕ��ג�R���Ȃ����āA�d��������鎞�ƁA���ג�R�������d��������Ȃ����Ƃł͓��삪�Ⴄ�̂͂Ȃ�ƂȂ�����܂������A��̓I�ɂ͂ǂ̂悤�Ȍ����łǂ�����ė���̂ł��傤���B
�Q���R�C���ɉ������ג�R���Ȃ����Ă��Ȃ����A�R�C���̗��[�ɂ͓d�����������Ă��܂��B���������������d���́A�ǂ��ɂ��������肪�����ĂуR�C���ɖ߂�܂��B