|
�傫�߂̕��i���A�������Ɣz�����ꂽ�^��ǃA���v�́A ����ȓd�C�̂����݂𗝉��������Ȃ�A�d�C�̓��发���Ă݂܂����B �Ƃ��낪�ǂ̖{���Ƒ������n�C�L���O�R�[�X����A�����Ȃ�~�R�o�R�ɂȂ邪���Ƃ��A �₳�������ȏ����o���X�^�C���͂����ɏ��������A �܂����������̃C���X�g���A�C���X�g���[�^�[�ƒ��҂Ƃ̃����N���キ�A �Ƃ����_���d�������A�d�C�̐��E�̒T���G�{�쐬��ڎw���܂����B |
![]()
�`�j�d�C��m��̂ɕK�v�ȂR�̕��i�i�R�v�f�j�́u�d�r�v�u�d���v�u��R��v
�@�@�@�P�@�d�r�́A�d�C�̂������Ɓu�d���v�������́B
�@�@�@�Q�@�d���́A�d�C�������ʂ蓹�ŁA�u�d���v������Ă��܂��B
�@�@�@�@�R�@�����Ē�R��́A�d�C�̗��������܂�����̂ƂȂ�A�����ʂ�u��R�v�ł��B
�Ƃ������ɏ������R�v�f�̂����A�P�ƂQ�͂���ƂȂ��킩����̂́A
�Ȃ��R�̂悤�ȁu����܂��́v���K�v�Ȃ̂ł��傤���B
�����A����ł͓d�C�̐��E�ɓ����Ă䂫�܂��傤�B
�a�j�d���Ƃ́H�E�E�E
�@���̎��⎩�́A���ɒP���ł͂���܂����A�[�I�ɐ������鎖�͈ӊO�Ɠ����������܂���B
�@�@���̂Ȃ琅���╗���͓���I�ɑ̊��o���܂����A�d���̓C���[�W���ɂ�������ł��B
���ɑ傫�ȗ������������ė��Ƃ��ƁA���������ŗ��ꗎ���܂��B
���������Ƃ́A�傫�ȃG�l���M�[�������A�厩�R�̗�ł́A��⌃��������ɂ�����܂��B
�@�@�@�@�@�@�@�@�@�@ �@�@�@
�@�@�@
�@�@�@�@�@�@
������܂藎���̖�����̉����Ȃǂ́A���̃G�l���M�[���������A����r�A�����܂�Ȃǂ́A�قƂ�ǃG�l���M�[�������Ƃ����܂��B
�@�@�@�@�@�@�@�@�@�@�@ �@�@
�@�@![]()
�@�@�@�@�@
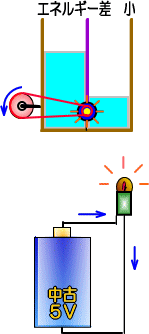
���̗�ł͍��፷�������A�������Ƃ���G�l���M�[���傫���Ƃ�����ł����A���l�ɓd���Ƃ́A
�@�d�C�̃G�l���M�[�̑傫���A�܂��@�d�C�𗬂����Ƃ���A�����̋����@������킵�A�P�ʂ�V�i�{���g�j�ŕ\���܂��B
�R���̓C�^���A�̃{���^�Ƃ��������w�҂̖��O���炫�Ă��܂��B
�b�j�d���Ƃ́H�E�E�E
�@��������̗�ɂ���Đ������܂��B
�d���͗��������̋����ł����A��������ʂ��厖�ł��B
�o�P�c�̐��t�ɂ���̂ɂP�t�ڂ͂U�O�b���������Ă����̂ŁA�Q�t�ڂ͂����ЂƂ����ӂ₵�A�����̂R�O�b�Ŗ��t�ɂȂ����Ƃ���ƁA
�@�P�b�Ԃ��Ƃɗ���o�鐅�̗ʂ��A�Q�{�ɑ��������ɂȂ�܂��B
 �@
�@ �@
�@
���l�ɁA�@�d���Ƃ͂P�b�Ԃɗ����d�C�̗��@���A�ǂ������\���Ă��āA�P�ʂ�A�i�A���y�A�j�ŕ\���܂��B
�R���̓t�����X�̃A���y�[���Ƃ��������w�҂̖��O���炫�Ă��܂��B
�d���͓d�C�𗬂����Ƃ��鋭���A�d���͂P�b�Ԃɗ����d�C�̗ʁB�ł͓d����W�����R�Ƃ́A�ǂ̂悤�Ȃ��̂ł��傤���B�@
�c�j��R�Ƃ́H
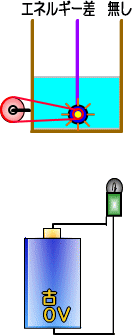
��́A�㗬�Ɖ����́A���፷�𐅂̃G�l���M�[�ɂ��āA�앝�ɂ݂��������̗ʂŗ���܂��B
�����ɐ��Ԃ�u���ƁA���Ԃ̉H���͐��̗���ɂԂ�����܂��B
��̐����炷��A���Ԃ̉H���́A����̂���܂��̂ł����A�������Ő��Ԃ͉��A���ꂪ���낢��Ȏd��������킯�ł��B
���l�ɓd�r�̃v���X�ƃ}�C�i�X�̊Ԃɓd�C�̗����W������̂�����ƁA�d�C�͔M����⎥�ƂȂ��Ďd�������܂��B
�܂��@��R�Ƃ́A�d�C�����ꂽ���ɁA�G�l���M�[�������o���A�d�������Ă��炤�ꏊ�@�ŁA�P�ʂ����i�I�[���j�ŕ\���܂��B
�R���̓h�C�c�̕����w�҃I�[�����炫�Ă��܂��B
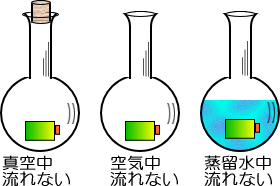
�Ƃ���œd�r�Ɏ��������闝�R�́A��łȂ������A�d��̂��鐅���ł���킹�܂��B
�}�̂悤�ɁA�v���X������o�Ă����d�C���A���[�^�[�ⓤ�d���̒��𗬂ꂽ��}�C�i�X���ɒ��܂��āA
�v���X�ƃ}�C�i�X�̃G�l���M�[�����Ȃ��Ȃ邩��ł��B
 �@
�@
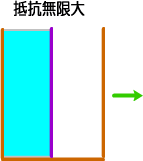
�d�r�ɉ����Ȃ��Ȃ����Ƃ́A�v���X�E�}�C�i�X�ԂɁA��C�Ƃ����d�C�̗���Ȃ������i�≏�́j���Ȃ����ꍇ�ŁA
�Ȃɂ��d�������܂���B
 �@
�@
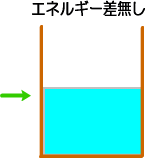
�@�܂��A�d�r�̃v���X�ƃ}�C�i�X�ړd���ŃV���[�g���������́A��C�ɑ�ʂ̓d��������A
�@�d�r�͂����Ƃ����ԂɎg���Ȃ��Ȃ�܂��B����͒�R���[���̎��ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@

�@��R�͖�����łः[���ł��A���̃G�l���M�[�������ʓI�Ɏ��o�������o�����A�Ӗ�������܂���B
�@�������A���悢�l�̎��ɂ́A���܂����p�ł��܂��B
�@�܂��A�V�i�̓d�r�ł��A�G�l���M�[���������Ȃ��悤�Ȑڑ��ł́A�d���͗���܂���B
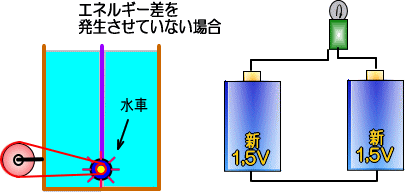
����ɓd�C�����̎p��ς��Ă��낢��ȋ@������Ă���̂ł͂Ȃ��A�d�C�̎����Ă���u�G�l���M�[���v
�������d�������Ă���̂��Ƃ�������Y��Ȃ��ʼn������B
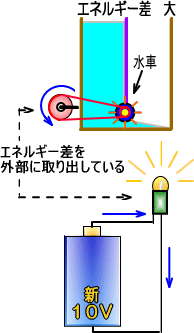
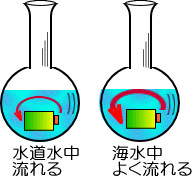
���͔��d���ł́A�_�����痎���鐅�̃G�l���M�[���ŁA���d�@�����܂��B
���̓_�����痎����������̂܂܂ł��B
�������̍��፷�����G�l���M�[���������d���������Ƃ����̂Ɠ����ł��B
�d�j�d�͂Ƃ́H
�@��̐����ɂ��āA�ǂ̂悤�ȏ�ԂȂ�A��葽���̎d�������邩�Ƃ�����
�@�@�@�@�@�@�@����鐨��������
�@�@�@�@�@�A�@�����ʂ�����
�@���̂悤�ȏꍇ�A�ǂ��炩���Q�{�ɂȂ�ƑS�̂��Q�{�ɂȂ�̂ŁA�|���Z�Ɠ����ɂȂ�܂��B
�@�����ŁA���̓���|�����킹�������u�d��������́v�Ƃ��܂��B�L���̓p���[�́u�o�v�ŕ\���A�P�ʂ͂v�i���b�g�j�ł��B
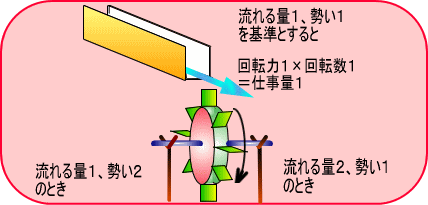
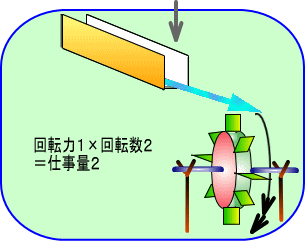 �@
�@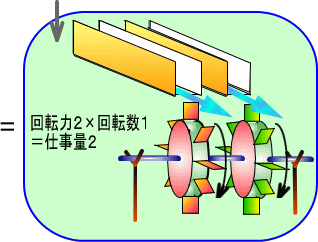
�@���b�g�̓C�M���X�̔����ƂŁA�d�C�ł͂Ȃ��@�B�̔��B�ɍv�������l�ł����A�p���[�̊T�O�͏��C�̗͂␅�̗͂����łȂ��A
�@�d�C�ɂ��p�����邱�ƂɂȂ�܂����B�ł�����d�C�ł̌v�Z���́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�u����鐨���v�~�u�����ʁv�A�@�@�܂�@�@�d���~�d�����d�́@�@�ł��B
�@����̐����ŁA�����₩�Ȑ�̉����̓G�l���M�[�����Ȃ��Ə����܂������A���ʂ��傫����A�S�̂̃G�l���M�[�͑傫���̂ł��B
�e�j�����ĕK�v�ƂȂ�I�[���̖@��
���̂悤�ȁ@�@�u��R���d�C�̎d���ꁁ�d�C�@��v�@�@�̗l�q���A�����ŕ\��������@�ɂ��āA�l���Ă݂܂��傤�B
�Ȃ������ŕ\������K�v�����邩�Ƃ����ƁA�u�X�Q�F�I�v�Ƃ��u�C�}�C�`�v�Ȃǂ̌��t�́A�m���ɕ��͋C�͂����܂��B
���������ꂪ���X�g�����̃��j���[�ŁA�l�i�̏��ɏ�����Ă����画�f�ł��Ȃ��̂Ɠ��l�ł��B
�܂��A�d�r�ɋ@����Ȃ������ɁA�u��R��v�Ƃ����֗��ȕ����g���܂��B
��R��͒Y�f�Ȃǔ�r�I�d�C�̗���ɂ��������̗��[�ɁA���̕��i���n���_�t�����邽�߂̓d���A�u���[�h���v�����t�������̂ł��B

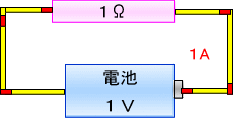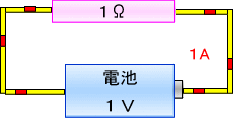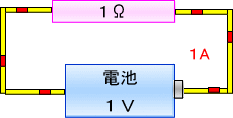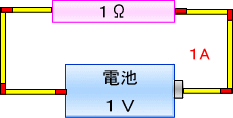
��R�̒P�ʁA�����u����ɂ����v�̒P�ʂ̓I�[���i���j�ł��B�ł͒�R��Ɠd�r�A�d�����g���āA���낢��ȗ�������܂��傤�B
�@�@�܂��g���̂͊�I�ȒP�ʂ������P�I�[���i�P���j����R���ł��B
 �@�@�@�@
�@�@�@�@
�܂��A���������w������d�r�̓d���͕��ʂP,�T�{���g�ł����A�l�������ȒP�ɂ���ׁA�P�u�i�{���g�j�Ƃ������Ƃ��܂��B
���̓d�r�ɒ�R����Ȃ������A�����d�����P�`�i�A���y�A�j�Ȃ�A���̒�R��͂P���i�P�I�[���j�Ƃ�������ɂ�������R�l�����A�ƌ��߂Ă��܂��܂��B
�i�l�p�̒��ŁA�d�C������ė����悤�ɂȂ��Ă���ׁA�d�C�̉��H�A�d�C��H�ƌĂт܂��B�j
���̎��o�Ă���P�{���g�ȊO�̂Q�̐��l�A�܂�P�I�[���ƂP�A���y�A���������킹���
�P�i�I�[���j�~�P�i�A���y�A�j���P�i�{���g�j
�@�Ƃ�����������t���邱�ƂɂȂ�܂��B
�܂��d�����P�I�[���̂Q�{����ɂ����Ȃ�悤�ɁA�Q�I�[���̒�R��Ɏ�芷����ƁA�d���́A�����̂O,�T�A���y�A�ɂȂ�܂��B
���̎��o�Ă���Q�̐��l�u�Q�v�Ɓu�O,�T�v���|���Z�����
�Q�i�I�[���j�~�O,�T�i�A���y�A�j���P�i�{���g�j
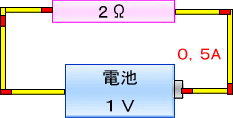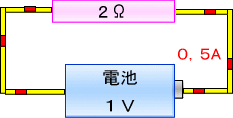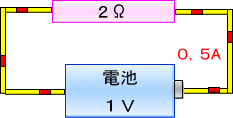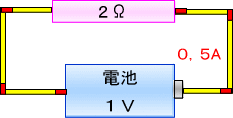
�@�ƌ���t���邱�ƂɂȂ�܂��B
�@����ɂP���{����ɂ������邽�߁A��R����P���I�[���ɂ���Γd���͂P�����̂P�A���y�A�ƂȂ�܂��B
���̎����o�Ă����Q�̐����u�P���v�Ɓu�P�����̂P�v���|���Z����ƁA
�@�@�@�@�P���i�I�[���j�~�P�����̂P�i�A���y�A�j���P�i�{���g�j
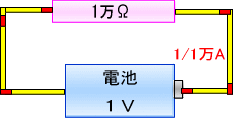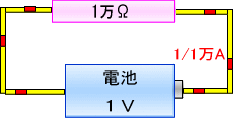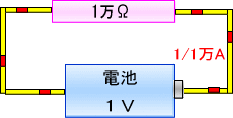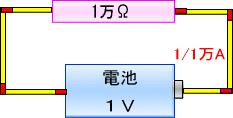
�@�Ƃ�����ɁA��R�Ɠd����������ƁA�������̓d���u�P�{���g�v��\���Ă��܂��B
�@�܂�@�@�@�@�@�@�@�u��R�v�~�u�d���v���u�d���v
�@�Ƃ����A�R�҂̊W���A�I�[���̖@���Ȃ̂ł��B
| �@�u�d���v�Ƃ������t���L���ŕ\�����鎞�́A�u�d�v�ŕ\���A��̓I�ȒP�ʂ̓{���g�u�u�v�Ŏ����܂��B �Ⴆ�Ί��d�r�̓d�����d�Ƃ��āA���ꂪ�P,�T�{���g���Ƃ����� �d���P,�T�u�@�@�Ə����܂��B �w�̍����ŗႦ��ƁA�����i�g�h�f�g�s�j�́u�g�v���A��̓I�ȒP�ʁu�����v�Ŏ����̂Ɠ����ŁA�g���P�U�O�Z���`�Ȃ� �g���P�U�O�����@�Ə����܂��B |
|
��������������A�̏d�̃E�F�C�g�i�v�d�h�f�g�s�j���u�v�v�ŕ\���A��̓I�ȒP�ʂ��u�j���v�Ŏ����̂Ɠ����ł� |
| �u��R�v�̓��W�X�^���X�́u�q�v�ŕ\���A��̓I�ȒP�ʂ̓I�[���u���v�Ŏ����܂��B |
�R�҂̊W�͎��̂R��ނ̎��ŕ\�����Ƃ��ł��܂��B
�Ƃ����Ă����͂P�̎����A�|���Z�⊄��Z�̖ŕό`���Ă��邾���ł��̂ŁA�ǂꂩ�P�����o���Ă���Ηǂ��ł��傤�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�u�h�~�q���d�v
���̎��̈Ӗ��́u�d���i�h�j�ƒ�R�i�q�j���|�����킹��ƁA��R�ɂȂ����d�r�̓d���i�d�j�ɂȂ�B�v�Ƃ������Ƃł�
�@�Ⴆ�A�Q�`�̓d�����T���̒�R�ɗ���Ă���Β�R�ɂȂ����Ă���d�r�̓d���d��
�@�@�@�@�@�@�@�@�@�@�@�@�Q�`�~�T�����P�O�u�@�ł��邱�Ƃ�����Ȃ��Ă��킩��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�A�u�d���q���h�v
���̎��̈Ӗ��́u�d���i�d�j���R�i�q�j�Ŋ���Β�R�ɗ���Ă���d���i�h�j�ɂȂ�B�v�Ƃ������Ƃł��B
�Ⴆ�P�O�u�̓d�r�ɂT�����Ȃ��Ɨ����d���h��
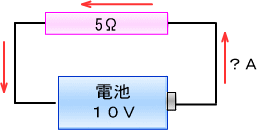
�P�O�u���T�����Q�`�ł��B
���e��������Ȃ��d�C��H�ŁA�T���Ə����Ă����R��̗��[�̓d�����e�X�^�[�Ōv���Ă݂���A�P�O�u�ł����B
�����ł��̒�R��ɂ́A�Q�`�̓d��������Ă��鎖�ɂȂ�܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�B�u�d���h���q�v
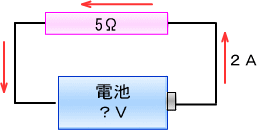
���̎��̈Ӗ��́u�d���i�d�j��d���i�h�j�Ŋ���Β�R�i�q�j�̑傫�����킩��B�v�Ƃ������Ƃł��B
�Ⴆ�P�O�u�̓d�r��Ȃ���R�ɂȂ�����A�Q�`�̓d��������Ă���Β�R�̑傫���q�́@
�@
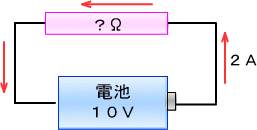
�q���P�O�u���Q�`���T���ł��B
�@����ɓd���Ɠd�����|�����킹�����̂�d�͂Ƃ����A�L���̓p���[�́A�o�P�ʂ̓��b�g�̂v�ŕ\���܂��B
�@��̐}�ł͂P�O�u�̓d�����Q�`����Ă���̂ŁA�d�͂o��
�o���P�O�u�~�Q�`���Q�O�v
�ƂȂ�܂��B�ƒ�p�̃R���Z���g�͂Q�O�O�O�v�܂Ŏg���āA�d���͂P�O�O�u�ł�����
�@�@�@�@�@�@�@�@�o���P�O�O�u�~�H�`���Q�O�O�O�v
�@�@�@�@�@�@�@�H�`���Q�O�O�O�v���P�O�O�u���Q�O�`�܂ŗ����邱�ƂɂȂ��Ă��܂��B
�y�Q�z���ɕ��ׂĂȂ��u����v�ƁA�P�{���ĂɂȂ���u����v�̂Q��ނɂ���
�@�@�`�j��R�̕���
�@
��R������ɕ��ׂĂ��ꂼ��ׂǂ����̃��[�h�����Ȃ������A��������ڑ��Ƃ��p�������ڑ��ƌĂт܂��B
�R���̒�R���R�{����ɂȂ��A���������P�{�̍�����R��̂悤�ɍl����ƁA���̒�R�l�͂R���̂P�̂P���ƂȂ�܂��B
�Ȃ��ł��傤���B
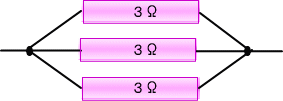
�@�@�@(�R�I�[���̒�R��R�{�����ڑ�����������R��j
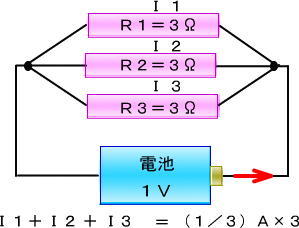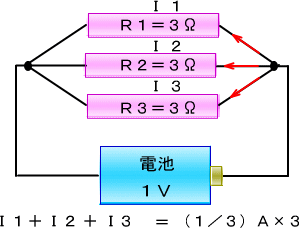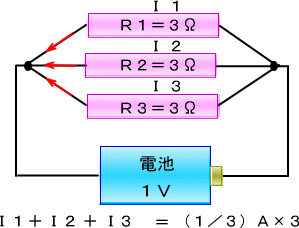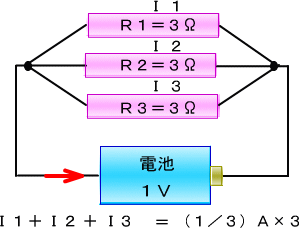
���Ƃ��P�u�̓d�r�ɂR���̒�R�i������q�P�Ƃ��܂��j���Ȃ��ƁA�����ɗ����d���@I�P�@�̒l��
�@�@�@�@�@�P�u���R�����i�P�^�R�j�`�@�ł��B
�����d�r�ɂ����P�A��͂�R���̒�R�A�q�Q���Ȃ��ƁA���̒�R�̒��ɗ����d���@I�Q�@�̒l��
�@�@�@�@�@�P�u���R�����i�P�^�R�j�`�@�ł�
����ɂ����P�A�R���̒�R�A�q�R���Ȃ��ł����̒�R�̒��𗬂��d��I�R�̒l�́A��͂�
�@�@�@�@�@�P�u���R�����i�P�^�R�j�`�@�ł�
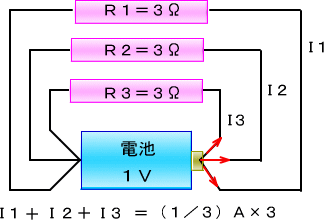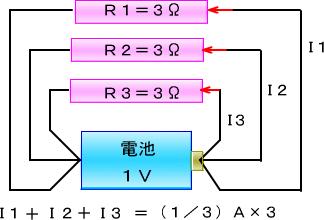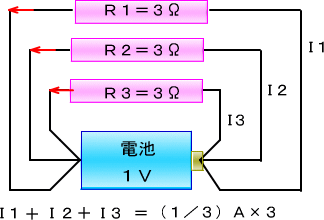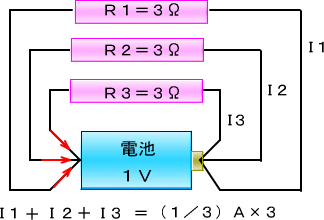
�����łq�P�Ƃq�Q�Ƃq�R�̓d�������킹���
�@�@�@�@�@�i�P�^�R�j�`�{�i�P�^�R�j�`�{�i�P�^�R�j�`���P�`�@
�ƂȂ�A���̍�����R�ɗ����d���͂P�`�A�܂�P�u�̓d�r�ɂP���̒�R���Ȃ������Ɠ����ɂȂ�܂��B
�����ł��̍�����R��͂P���ƍl���Ă��܂�Ȃ������킩��܂��B
�i�ꌩ����Ă݂��܂����O�̐}�Ɖ��̐}�͑S�������ڑ��ł��B�j
�Ƃ���ŁA����ǂ͂R���̂q�P�ƁA�Q���̂q�S�����ɂȂ�����A
���̂Q�{�łł��鍇����R��̒�R�͉��I�[���ɂȂ�ł��傤���B
�q�P�̓d���́@�@�@�P�u���R�����i�P�^�R�j�`
�q�S�̓d���́@�@�@�P�u���Q�����i�P�^�Q�j�`
�����łq�P�̓d���Ƃq�S�̓d�������킹���
�@�@�i�P�^�R�j�`�{�i�P�^�Q�j�`���i�T�^�U�j�`�@
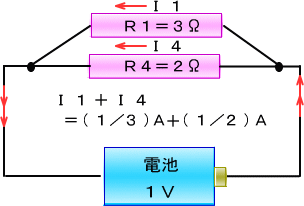
�P�u�̓d�r�����̍�����R��ɂȂ������ɗ��ꂽ�d�����i�T�^�U�j�`�Ȃ̂ŁA��R�l��
�@�@�@�@�P�u���i�T�^�U�j�`���i�U�^�T�j�����P,�Q���@�ƂȂ�܂��B
|
�@�@�@�@�P�A�܂��P�u�̓d�r�ɂȂ������̓d�����Z�o���邽�߁A���q���P(1V)�ŁA �@�@�@�@�Q�A���ɂ����̕����𑫂��Z���邱�Ƃɂ��A�d���̍��v�l���Z�o���܂��B �@�@�@�@�R�A�Ō�ɁA��R�͓d�����d���ł�����A�PV���d���l�܂蕪�q�ƕ���� |
�a�j��R�̒���
�@�@�@���ɁA��R����P�{�̐��ɂȂ�悤�Ȃ���ƁA�����ڑ��Ƃ��V���[�Y�ڑ��ƌĂт܂��B
![]()
�@�@�@�@�@�@�@�@�i�R���̒�R��R�{�̒���ڑ��j
�P�u�̓d�r�ɁA�R���̒�R�q�P�A�q�Q�A�q�R���R����ɂȂ��ƁA�d��������܂��B
���̏�Ԃ͓�������ЂƂA�o�����ЂƂ̂P�{���Ȃ̂ŁA�r�����瑝�����茸�����肷�邱�Ƃ͂��肦�܂���B
�܂�A�ǂ̒�R�ɂ������d�����ʂ�܂��̂ŁA���̓d�����Ƃ肠����I�Ƃ��܂��B
����ƁA�q�P�̗��[�̓d���ͤ�d���ƒ�R�̊|���Z��
�@�@�@�@�@�@�d�P��I�~�R���@������d�P�Ƃ��܂�
�q�Q�̗��[�ɋN����d���d�Q��
�@�@�@�@�@�@�d�Q��I�~�R��
�q�R�̗��[�ɋN����d���d�R��
�@�@�@�@�@�@�d�R��I�~�R��
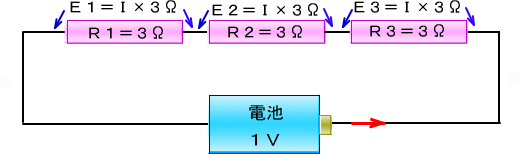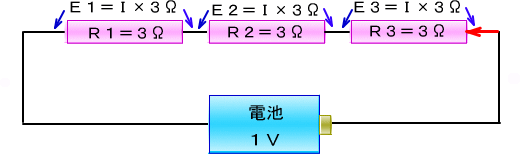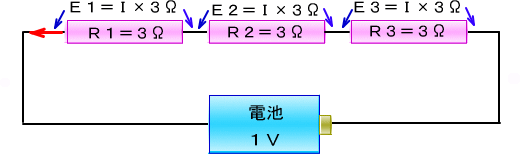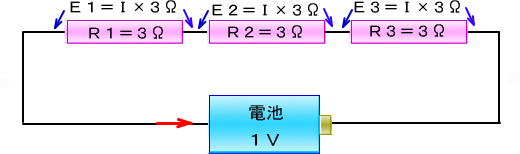
���̂Ƃ��R�̓d����S�����킹�����̂��A���Ƃ̓d�r�̓d���P�u�ɂȂ����Ă��܂�����
�@�@�@�@�@�d�P�{�d�Q�{�d�R���P�u
������
�@�@�@�@�@�d�P�{�d�Q�{�d�R���iI�~�R���j�{�iI�~�R���j�{�iI�~�R���j
�@�@�@�@�@�@�@�@��I�~�i�R���{�R���{�R���j
�@�@�@�@�@�@�@�@��I�~�X��
�@�@�@�@�@�@�@�@���P�u
�@�ƂȂ��ēd��I�͂P�u�ɂX�����Ȃ������Ɠ������ƂɂȂ�܂��B
�����Œ�����R��
�@�@�@�q�P�{�q�Q�{�q�R���X��
�@�Ƃ����P���ȑ����Z�ŋ��߂Ă��ǂ��悤�ł��B
�@�܂����̎��d���h��
�@I���P�u���X�����i�P�^�X�j�`�@�ƂȂ肻���ł��B
�@�Ƃ���łR���̂q�P�ƂQ���̂q�S��ɂ�����ǂ��Ȃ�ł��傤���B
�@�����łƂ肠�������̂P�{���ɗ����d����I�Ƃ��čl����ƁA
�@�q�P���[�̓d���́@�@�d�P��I�~�R��
�@�q�S���[�̓d���́@�@�d�S��I�~�Q��
�@�d�P�Ƃd�S�𑫂����d�����A�d�r�̓d���P�u�Ȃ̂�
�@�@�@�@�@�d�P�{�d�S���iI�~�R���j�{�iI�~�Q���j
�@�@�@�@�@�@�@��I�~�i�R���{�Q���j
�@�@�@�@�@�@�@��I�~�T��
�@�@�@�@�@�@�@���P�u
�@�ƂȂ��ēd��I�͂P�u�ɂT�����Ȃ������Ɠ����ɂȂ�܂�����
�@������R�̒l�͒P���ɑ����Z����Ηǂ������킩��܂��B
�@���Ȃ݂ɓd��I���v�Z�����
�@�@�@�@I���P�u���T�����O,�Q�`�@�@�ł��B
�@
�b�j�d�r�̕���
�@�P,�T�u�̓d�r�̃v���X�ǂ����A�}�C�i�X�ǂ������Ȃ��ĕ���ڑ��ɂ��A���[�̓d���𑪂��Č���ƁA
�@������ɂ��Ă��P,�T�u�̂܂܂ŕς��܂���B
�d�����ς��Ȃ��̂ɁA�d�r����������Ȃ���̂́A�ꌩ���ʂȂ悤�ł����A���̕��d�������������܂��B
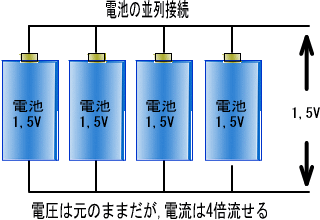
����͈�ʉƒ�̓d�C����ʂ�������ɘA��āA���d�����������݂���̂Ɠ����ł��B
���d���������Ă��R���Z���g�̓d���������Ȃ�킯�ł͂���܂���B
��葽���̓d�C���i���Ȃ�����悤�ɂȂ�A
�@�܂肽������d����������悤�ɂ��Ďg����d�͂𑝂₷�Ƃ������Ȃ̂ł��B
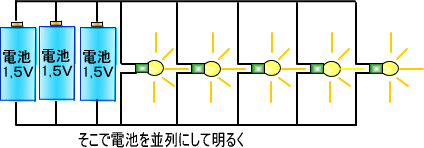
�d�r�͂�����ł��d����������킯�ł͂���܂���B
�@�Ⴆ�V�i�̓d�r�ł���ʂɓd���𗬂��Ɠd�����������Ă��܂��܂��B
���̂悤�Ȏ��A�d�r�̕���ڑ������ʓI�ɂȂ�܂��B
�d�C�̎��ۂ̎d���͓d���Ɠd�����|�����킹���d�͂Ŏ����܂����A
�@���̏ꍇ�͓d�������œd�����������ꍇ�̗�ł��B
�c�j�d�r�̒���
���ɓd�r���c�ɐςݏグ��悤�ɒ���ڑ�����ƁA���[�̓d���͐ςݏグ���d�r�̐����������čs���܂��B
�P,�T�u�̓d�r�Ȃ�Q�łQ�{�̂R�u�A�P���Ȃ�P���{�̂P���T��u�ɂȂ�܂��B
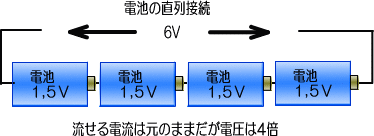
�@������������d���͂P�̂Ƃ��Ɠ����ł��B���̏ꍇ�d���𑝂₷���Ƃɂ���ēd�͂����������ƂɂȂ�܂��B
�@�d�����P���{�ɂ�������A�P�������d�r���P�̓d�r�ƌ����ĂāA������P������ɂ���Ηǂ��킯�ł��B
�@���̎��K�v�ȓd�r�͂P���~�P�����P���ɂȂ�A�d�͂��P���{�ɂȂ�܂��B

